边缘协作环境下最小化完工时间任务调度方法

张超; 赵辉; 张智峰; 王静; 万波; 王泉

doi:10.19665/j.issn1001-2400.20240308

English Version

您当前的位置：

首页 >

文章列表页 >

边缘协作环境下最小化完工时间任务调度方法

计算机科学与技术 & 网络空间安全 | 更新时间：2024-11-13

- 边缘协作环境下最小化完工时间任务调度方法
- Task scheduling method for minimizing completion time in edge collaborative environment
- 角色： First author , 第一作者 ,
  
  机构：
  西安电子科技大学计算机科学与技术学院,陕西西安 710071
  陕西省智能人机交互与可穿戴技术重点实验室,陕西西安 710071
  
  邮箱： 22031212431@stu.xidian.edu.cn
  
  简介： [ "张超(2000—),男,西安电子科技大学硕士研究生,E-mail:22031212431@stu.xidian.edu.cn" ]
  
  暂无本作者相关信息
  张超
  12 ，
  角色：
  
  机构：
  西安电子科技大学计算机科学与技术学院,陕西西安 710071
  陕西省智能人机交互与可穿戴技术重点实验室,陕西西安 710071
  
  邮箱： hzhao@mail.xidian.edu.cn
  
  简介： [ "赵辉(1983—),男,副教授,博士,E-mail:hzhao@mail.xidian.edu.cn" ]
  
  暂无本作者相关信息
  赵辉
  12 ，
  角色：
  
  机构：
  西安电子科技大学计算机科学与技术学院,陕西西安 710071
  
  邮箱： 20181214346@stu.xidian.edu.cn
  
  简介： [ "张智峰(1998—),男,西安电子科技大学硕士研究生,E-mail:20181214346@stu.xidian.edu.cn" ]
  
  暂无本作者相关信息
  张智峰
  1 ，
  角色： Corresponding author , 通讯作者 ,
  
  机构：
  西安电子科技大学计算机科学与技术学院,陕西西安 710071
  
  邮箱： wangjing@mail.xidian.edu.cn
  
  简介：王静(1981—),女,副教授,博士,E-mail:wangjing@mail.xidian.edu.cn
  
  暂无本作者相关信息
  王静
  1 ，
  角色：
  
  机构：
  西安电子科技大学计算机科学与技术学院,陕西西安 710071
  陕西省智能人机交互与可穿戴技术重点实验室,陕西西安 710071
  
  邮箱： wanbo@xidian.edu.cn
  
  简介： [ "万波(1976—),男,教授,博士,E-mail:wanbo@xidian.edu.cn" ]
  
  暂无本作者相关信息
  万波
  12 ，
  角色：
  
  机构：
  西安电子科技大学计算机科学与技术学院,陕西西安 710071
  陕西省智能人机交互与可穿戴技术重点实验室,陕西西安 710071
  
  邮箱： qwang@xidian.edu.cn
  
  简介： [ "王泉(1970—),男,教授,博士,E-mail:qwang@xidian.edu.cn" ]
  
  暂无本作者相关信息
  王泉
  12 ，
- 西安电子科技大学学报 2024年51卷第4期页码：114-127
- 作者机构：
  
  1. 西安电子科技大学计算机科学与技术学院,陕西西安 710071
  2. 陕西省智能人机交互与可穿戴技术重点实验室,陕西西安 710071
- 作者简介：
  
  [ "张超(2000—),男,西安电子科技大学硕士研究生,E-mail:22031212431@stu.xidian.edu.cn" ]
  [ "赵辉(1983—),男,副教授,博士,E-mail:hzhao@mail.xidian.edu.cn" ]
  [ "张智峰(1998—),男,西安电子科技大学硕士研究生,E-mail:20181214346@stu.xidian.edu.cn" ]
  王静(1981—),女,副教授,博士,E-mail:wangjing@mail.xidian.edu.cn
  [ "万波(1976—),男,教授,博士,E-mail:wanbo@xidian.edu.cn" ]
  [ "王泉(1970—),男,教授,博士,E-mail:qwang@xidian.edu.cn" ]
- 基金信息：
  
  陕西省重点研发计划(2024GX-YBXM-010);陕西省重点研发计划(2024GX-YBXM-140);陕西省重点研发计划(2024GX-YBXM-039);中央高校基本科研业务费专项资金(ZYTS24089)
- DOI：10.19665/j.issn1001-2400.20240308
  中图分类号： TP301.6
- 纸质出版日期：2024-08-20，
  
  网络出版日期：2024-04-07，
  
  收稿日期：2023-09-28，
- 稿件说明：
移动端阅览
引用本文

阅读全文PDF
张超, 赵辉, 张智峰, 等. 边缘协作环境下最小化完工时间任务调度方法[J]. 西安电子科技大学学报, 2024,51(4):114-127.

Chao ZHANG, Hui ZHAO, Zhifeng ZHANG, et al. Task scheduling method for minimizing completion time in edge collaborative environment. [J]. Journal of Xidian University, 2024,51(4):114-127.
张超, 赵辉, 张智峰, 等. 边缘协作环境下最小化完工时间任务调度方法[J]. 西安电子科技大学学报, 2024,51(4):114-127. DOI： 10.19665/j.issn1001-2400.20240308.

Chao ZHANG, Hui ZHAO, Zhifeng ZHANG, et al. Task scheduling method for minimizing completion time in edge collaborative environment. [J]. Journal of Xidian University, 2024,51(4):114-127. DOI： 10.19665/j.issn1001-2400.20240308.

边缘协作环境下最小化完工时间任务调度方法

张超 ; 赵辉 ; 张智峰 ; 王静 ; 万波 ; 王泉 ;

PDF下载

摘要

由于用户地理位置分布不均可能导致边缘服务器负载不均衡,难以为用户提供满意的服务质量。此外,边缘服务器可用资源有限,一些大任务可能难以全部卸载到边缘服务器。针对以上问题,利用多个边缘服务器之间的协作,结合任务部分卸载方式,提出一种边缘协作环境下最小化完工时间的任务调度方法。首先,结合边缘水平协作和任务部分卸载技术,考虑多用户多边缘服务器场景下用户和边缘服务器的位置关系,以最小化任务完工时间为目标,建立任务部分卸载调度模型;其次,提出基于改进分组教学优化算法的任务调度算法,联合优化边缘服务器计算资源分配、用户-边缘服务器关联决策、任务卸载比例以及执行位置决策,以最小化任务完工时间为目标,实现边缘计算环境下任务的高效调度;最后,通过实验将提出的任务调度算法与其他算法在多个指标下进行对比。实验结果表明,所提方法能够有效降低任务完工时间。

译

Abstract

The uneven geographical distribution of users may lead to unbalanced load on edge servers,which makes it difficult to provide satisfactory service quality for users.In addition,the available resources of the edge server are limited,and some large tasks may be difficult to offload to the edge server.To solve the above problems,this paper proposes a task scheduling method to minimize the completion time in the edge collaboration environment by utilizing the collaboration among multiple edge servers and combining the task partial offloading technology.First,by combining the edge of horizontal collaboration and task partial offloading technology and considering the position relationship between users and edge servers in multi-user multi-edge server scenario,a task partial offloading and scheduling model is established to minimize the task completion time.Second,a task scheduling algorithm based on the Improved Group Teaching Optimization Algorithm(IGTOA) is proposed to jointly optimize the edge server computing resource allocation,user-edge server association decision,task offloading ratio and execution location decision.With minimizing the task completion time as the goal,efficient task scheduling is achieved under edge computing environment.Finally,the proposed task scheduling algorithm is compared with DTOSO,HJTORA and ACS algorithms under multiple indexes.Experimental results show that the proposed method can effectively reduce the task completion time.

译

关键词

边缘协作; 部分卸载; 调度算法; 分组教学优化算法

译

Keywords

edge collaboration; partial offloading; scheduling algorithm; group teaching optimization algorithm

译

1 引言

随着5G通信和物联网技术的发展与普及,传统中心云难以实时响应海量的服务请求,需要将大量数据处理从数据中心下沉到网络边缘。边缘计算通过将服务聚集部署到更靠近用户的边缘,能够减少数据的往返时延,从而实时响应用户请求。

译

然而,边缘计算环境下用户的地理位置呈分布式、边缘服务器无线网络的接入范围有限等,导致不同边缘服务器的负载很不均衡。重负载的边缘服务器面对分布式、多用户设备的计算密集型任务请求时,难以提供令人满意的服务质量,影响用户的服务体验^[

1]。

译

由于边缘服务器和中心云都可以提供计算服务,且中心云有丰富的计算资源,一些研究者提出云-边-端三层协作架构的垂直卸载方式,在边缘服务器资源不足的情况下,将任务卸载到中心云执行。但这种垂直协作方案带来两个缺点:一方面,将任务卸载到中心云可能会导致延迟时间较长,无法满足一些对延迟敏感的任务的时间要求;另一方面,由于不同边缘服务器的负载不均衡,一些边缘服务器可能处于空闲状态,造成资源的浪费。将本区域内的一部分任务通过协作的方式转发到邻近的边缘服务器上执行,实现边缘服务器负载均衡,可以提高系统全局的性能。因此,考虑边缘服务器之间的协作来研究边缘计算环境下的任务调度是一种很有前景的调度方式。

译

先进的调度策略和技术对于实现边缘计算资源的优化调度,从而满足终端设备和系统的服务质量要求是必不可少的。近年来,出现了许多优秀的资源调度技术。根据是否需要控制中心收集全局信息,资源调度可以分为集中式或分布式。通常,集中式方法主要包括凸优化、启发式算法和机器学习等算法;分布式方法主要包括博弈论、匹配理论、拍卖、联邦学习等算法。由于用户以及服务资源是分布式部署的,为了统筹全局服务器异构资源,根据用户需求灵活分配计算资源,轻量级、集中式的任务卸载与任务调度框架能够有效利用分散资源,提高资源的利用率。

译

另外,根据任务的卸载方式,可以将任务卸载方式分为二进制卸载(Binary Offloading)与部分卸载(Partial Offloading),不同的任务卸载方式对系统整体性能也会有不同的影响。由于任务的异构性,任务的大小差异很大,有些大任务难以全部卸载至边缘服务器。与二进制卸载方式相比,部分卸载方式可以根据用户需求灵活地调整卸载比例,充分利用本地和边缘服务器的资源,带来更低的响应时间。

译

基于上述分析,文中提出了一种边缘协作环境下的任务调度方法,通过边缘服务器之间的协作与任务部分卸载技术实现最小化任务完工时间。首先,根据边缘服务器的网络拓扑以及用户与边缘服务器的位置关系,以最小化任务完工时间为目标,建立边缘协作环境下任务部分卸载与调度模型;其次,建立计算资源分配、用户-边缘服务器关联决策、任务卸载比例以及任务执行位置决策联合优化问题,根据优化问题的非凸性,采用固定变量和子问题分解的方式,并结合改进的分组教学优化算法(Improved Group Teaching Optimization Algorithm,IGTOA),提出一种任务调度迭代寻优策略;最后,通过实验验证所提出算法的有效性。文中的主要贡献如下:

译

(1) 建立了边缘协作环境下任务部分卸载与调度模型。考虑边缘服务器间拓扑结构、负载和任务属性,定义边缘协作环境下任务转发时间模型以及任务在本地和边缘服务器执行的时间模型,以最小化任务完工时间为目标,建立边缘协作环境下任务部分卸载优化问题。

译

(2) 提出了基于改进分组教学优化算法的任务调度算法。分析了时间优化问题的复杂性,采用子问题分解方式,将分组教学优化算法与计算资源分配策略、用户-边缘服务器关联策略相结合,迭代解决调度问题,从而得到最优的任务调度决策。

译

2 相关工作

移动边缘计算能够为移动终端提供距离更近的服务资源,按照协作方式可以划分为垂直卸载和水平卸载。垂直卸载协作方式具体可分为:边-端两层协作和云-边-端三层协作。宋宇波等^[

2]提出了一个基于边缘服务器和车载服务器协同工作的任务卸载策略及安全协商机制,在保证通信安全的同时降低了系统能耗。YUAN等^{[参考文献 3

百度学术

3]}将远程中心云作为边缘层的补充,综合考虑边缘计算层的CPU、内存、带宽资源限制、负载均衡以及异构节点的处理能力,共同优化中心云和边缘层的任务卸载与资源分配。DING等^{[参考文献 4

百度学术

4]}在多用户多边缘服务器的场景下使用云-边-端三层协作方式,构建博弈使每个节点都自私地最小化其设备能耗与任务响应时间。然而,在垂直卸载方式下将任务卸载到中心云会导致延迟时间较长,并且由于请求的异构性或用户分布不均匀,可能导致部分边缘节点负载较重,邻近的边缘节点负载较轻,造成资源的浪费。

译

在水平卸载协作方式中,多个边缘服务器之间可相互协作为用户提供服务,解决部分边缘服务器资源不足的问题^[

5],提高任务执行效率和用户服务质量。赵辉等^{[参考文献 6

百度学术

6]}考虑未知性能节点可能导致任务执行时间或传输时间过长的问题,以能耗优化为目标,提出了一种面向边缘计算平台的半在线任务动态调度方法。彭青蓝等^{[参考文献 7

百度学术

7]}针对可协作的边缘服务器提出了去中心化的在线任务调度算法,由实时任务调度策略、边缘资源分配策略和运行时任务迁移策略组成,有效降低了加权任务响应时间。然而,由于任务的异构性,任务的大小差异很大,有些大任务难以全部卸载至边缘服务器,从而影响系统性能。

译

从任务是否全部卸载角度看,任务卸载方式可分为二进制卸载和部分卸载。WANG等^[

8]研究多用户单服务器场景下的二进制卸载问题,并提出了一个迭代优化算法,有效降低了系统的加权和延迟。邝祝芳等^{[参考文献 9

百度学术

9]}应用深度强化学习解决单服务器多任务调度问题,降低了延迟和本地能耗。由于边缘服务器计算资源的限制,与二进制卸载方式相比,部分卸载方式可以根据用户需求灵活地调整卸载比例,充分利用本地和边缘服务器的资源。NING等^{[参考文献 10

百度学术

10]}提出一个5G车载网络的部分卸载和自适应任务调度框架,通过双边匹配算法和凸优化理论求解最优的信道资源分配策略与卸载比例,使用户和服务提供商之间的利益达到均衡。MALIK等^{[参考文献 11

百度学术

11]}研究了多用户单服务器场景下无线充电与任务卸载调度问题,以最小化计算卸载的能量消耗和最大化用户从无线充电中接收到的能量为目标,基于凸优化理论设计并实现了低复杂度算法。

译

在集中式任务卸载与资源调度方式中,已有不少工作将启发式算法和深度强化学习方法用于求解混合整数规划问题。ZHANG等^[

12]用局部搜索启发式算法解决多分布式虚拟机场景下的联合工作负载分配和计算频率配置问题,有效降低了系统能耗。HU等^{[参考文献 13

百度学术

13]}将边缘计算中的请求调度问题表述为混合整数非线性规划,并将该问题看作为一个双重决策问题,提出了一种基于多目标遗传算法的优化方法来解决该问题。ELGENDY等^{[参考文献 14

百度学术

14]}提出基于强化学习的多用户单服务器二进制任务卸载与缓存算法。实验表明,该算法在边缘服务器上卸载和缓存任务可以显著节省能量和时间。LIU等^{[参考文献 15

百度学术

15]}针对物联网边缘计算系统中的任务卸载问题,根据用户优先级为用户分配边缘服务器,并使用深度强化学习技术来学习最优策略。

译

上述研究从协作方式、卸载方式以及算法设计方面实现了边缘计算环境下的任务卸载,但它们都没有结合边缘水平协作和任务部分卸载的优势,未能充分利用相邻边缘服务器的资源。在密集部署的网络环境下,相邻边缘服务器的覆盖区域通常是相交的,意味着处在重叠区域的用户可以访问覆盖他们的任何边缘服务器。此外,用于边缘计算的机器学习技术虽然有强大的学习能力,但需要大量参数,并且输出结果难以解释,可信度较低。因此,需要同时考虑是否卸载、卸载时关联的边缘服务器及卸载时使用的算法类型,以便更好地利用边缘服务器资源,提高任务调度效率。针对上述问题,文中建立了边缘协作环境下的任务部分卸载与调度模型,并提出了一种基于改进分组教学优化算法的任务调度算法。

译

3 边缘协作环境下的任务部分卸载与调度模型

考虑边缘服务器集合为M={1,2,…,m},每台边缘服务器可以为其覆盖范围内的移动设备提供任务卸载与执行服务。边缘服务器网络的拓扑结构用图G={V,E}表示,其中V={v_j|j∈M}表示边缘服务器节点及所在位置;E={e_jk|j,k∈M}表示边缘服务器j和k的有线链接;e_jk表示有线链接的带宽,e_jk=0表示两个边缘服务器间没有链接,假设边缘服务器之间的有线链接是双向的,当j≠k时,e_jk=e_kj;当j=k时,e_jk=$ +\infty $。用户设备集合定义为N={1,2,…,n},随机分布在边缘服务器的覆盖范围内。用户设备i生成的计算任务表示为X_i={u_i,s_i}(i∈N),u_i表示任务输入数据的大小,单位为bit,s_i表示任务被CPU处理的计算量大小;任务X_i可以在本地处理,也可以将部分卸载到边缘执行。定义δ_i(0≤δ_i≤1)为卸载到边缘服务器上执行的比例,任务在本地和边缘服务器上并行执行,其中(1-δ_i)s_i在本地执行;δ_is_i为卸载到可直接接入的边缘服务器上执行,或通过边缘服务器之间的协作,转发到非本地接入范围内的边缘服务器上执行。

译

定义A表示用户与边缘服务器的关联决策变量集合,a_ij(i∈N,j∈M)表示用户设备i与边缘服务器j的关联决策变量,a_ij=1表示将用户设备i占用边缘服务器j的无线信道进行数据上传, $\sum_{j = 1}^{|M|}$ a_ij=0表示任务在本地执行。定义B表示任务在边缘服务器的执行决策变量集合,b_ij(i∈N,j∈M)表示任务最终执行位置的决策变量,b_ij=1表示任务在边缘服务器j上执行,否则b_ij=0。定义Θ_j={i|i∈N,j∈M,a_ij=1},表示占用边缘服务器j无线信道传输数据的任务集合。边缘服务器的负载随任务卸载量的增加而增加,定义Φ_j={i|i∈N,j∈M,b_ij=1},表示最终在边缘服务器j上执行的任务集合。

译

用户设备i的CPU频率用 $f_{i}^{l}$ 表示,在本地执行的任务大小为(1-δ_i)s_i,那么任务在本地执行部分的执行时间为

译

T_{i}^{l}

=(1-δ_i)

\frac{s_{i}}{f_{i}^{l}}

。

(1)

将任务部分卸载到边缘服务器的执行时间由3部分组成:任务数据上传时间 $T_{i}^{u p}$ 、协作执行时边缘服务器之间的任务数据转发时间 $T_{i}^{t r a n s}$ 以及任务的边缘计算时间 ${T^{e}}_{i}$ 。假设接入同一边缘服务器的用户在传输数据时互不干扰,传输通道在同一个卸载执行周期内保持不变,为关联到同一台边缘服务器的用户分配正交频谱,任务数据上行的无线链路传输速率r_ij定义为

译

r_ij=W_ijlb

(1 + \frac{p_{i} h_{i j}}{N_{0}})

(2)

其中,p_i表示任务i上传时的传输功率,N₀表示高斯背景噪声功率。W_ij表示边缘服务器j分配给用户设备i的传输带宽,定义为

译

W_ij=

\frac{W_{j}}{|Θ_{j}|}

(3)

其中,W_j表示边缘服务器j的最大无线带宽, $|Θ_{j}|$ 表示边缘服务器j关联的用户数量。h_ij表示用户设备i所在位置和边缘服务器j之间的无线上行链路信道增益,由用户i与边缘服务器j间的距离表示,即

译

$h_{i j}=\left\{

\begin{array}{l} d_{i j}^{- β}, d_{i j} ⩽ l_{j} \\ 0, d_{i j} > l_{j} \end{array}

\right.$

(4)

其中,d_ij表示用户设备i和边缘服务器j之间的距离,β为路径损失因子,l_j表示边缘服务器j无线信号的覆盖半径。由式(4)可知,当用户不在边缘服务器的覆盖范围时,信道增益为0,此时用户不可接入。当用户与边缘服务器距离越近,信道增益越大,无线传输速率也越大。结合式(2),用户任务的数据上传时间 $T_{i}^{u p}$ 定义为

译

T_{i}^{u p}

\sum_{j = 1}^{|M|}

a_ij

\frac{δ_{i} u_{i}}{r_{i j}}

。

(5)

基于边缘协作环境下的网络模型,定义边缘服务器j和k的最短路径为P_j_,_k。结合用户-边缘服务器关联决策变量和任务执行位置决策变量,将任务转发路径与边缘服务器间最短路径关联起来,任务X_i转发的路径Ω_i为

译

Ω_i=a_ijb_ikP_j_,_k 。

(6)

假设每个决策制定期间边缘服务器之间的带宽状况不变,与文献[

16]类似,文中假设边缘服务器之间的传输速率高、卸载的请求小,由并发传输任务导致的时间冲突可忽略不计,同时由于协作发生在相邻近的边缘服务器间,传播延迟可忽略不计。边缘服务器之间任务转发传输时间为

译

T_{i}^{t r a n s}

\sum_{j = 1}^{|M|} \sum_{k = 1}^{|M|} \sum_{e_{j k} \in Ω_{i}}^{} \frac{δ_{i} u_{i}}{e_{j k}}

。

(7)

假设δ_i比例的任务最终被卸载到边缘服务器j上执行,边缘服务器j为任务分配的计算资源用 $f_{i j}^{e}$ 表示。任务X_i在边缘服务器执行的时间 ${T^{e}}_{i}$ 为

译

{T^{e}}_{i}

\sum_{j = 1}^{|M|}

b_ij

\frac{δ_{i} s_{i}}{f_{i j}^{e}}

。

(8)

结合式(5)、(7)、(8),任务卸载到边缘执行的总时间可表示为

译

T_{i}^{o f f}

\sum_{j = 1}^{|M|} [\frac{a_{i j} δ_{i} u_{i}}{W_{i j} l b (1 + \frac{p_{i} h_{i j}}{N_{0}})} + \sum_{k = 1}^{|M|} (\sum_{e_{j k} \in Ω_{i}}^{} \frac{δ_{i} u_{i}}{e_{j k}} + b_{i k} \frac{a_{i j} δ_{i} s_{i}}{f_{i k}^{e}})]

。

(9)

将任务划分为本地执行部分和边缘服务器执行部分,二者并行执行,并且本地执行占用CPU资源,数据上行卸载占用I/O资源,通信与计算互不干扰。任务X_i的执行时间T_i为本地执行和边缘卸载执行时间的最大值:

译

T_i=max{

T_{i}^{l}

T_{i}^{o f f}

} 。

(10)

将所有用户任务执行时间定义为函数T:

译

T(A,B,δ,F)=

\sum_{i = 1}^{|N|}

T_i 。

(11)

以最小化所有用户任务执行时间为目标,联合优化用户-边缘服务器关联决策A、任务执行位置选择决策B,任务卸载比例决策δ以及边缘服务器资源分配F的优化问题P1定义为

译

P1:

\underset{A, B, δ, F}{m i n}

(12)

s.t. a_ij∈

\{0,1\}

,∀i∈N,j∈M,

(12a)

b_ij∈

\{0,1\}

,∀i∈N,j∈M,

(12b)

\sum_{j = 1}^{|M|}

a_ij≤1,∀i∈N,

(12c)

\sum_{j = 1}^{|M|}

b_ij≤1,∀i∈N,

(12d)

0≤δ_i≤1,∀i∈N,

(12e)

f_{i j}^{e}

≥0,

(12f)

\sum_{i \in Θ_{j}}^{} f_{i j}^{e}

≤F_j 。

(12g)

约束式(12a)和式(12c) 表示用户要么本地执行,要么只能关联最多一个边缘服务器进行任务卸载;约束式(12b)和式(12d)表示每个任务只能本地运行或选择最多一个边缘服务器与本地并行执行任务;约束式(12e)表示任务卸载比例限制,δ_i=1表示二进制卸载,δ_i=0表示任务只在本地执行;约束式(12f)和式(12g)表示在每个边缘服务器上给执行任务分配的资源总和不能超过其总计算资源。通过分析可知,问题P1是一个大规模的混合整数非线性规划问题,寻找最优解通常需要指数时间复杂度,无法通过多项式时间算法求得最优解,可通过子问题分解结合改进的元启发式算法求解问题。

译

4 基于改进分组教学优化算法的任务调度算法

在该优化问题中需要同时求解4个变量,元启发式算法被广泛应用于此类问题的求解。然而,根据约束条件直接对四维变量进行搜索将产生大量不可行的解。因此,文中通过变量固定的方式,将原问题P1分解成子问题,通过计算资源分配策略、用户-边缘服务器关联策略、任务卸载执行位置和卸载比例搜索算法交替迭代求解。

译

首先,在改进的分组教学优化算法中初始化任务执行位置B和卸载比例δ;其次,根据初始化的任务执行位置B和卸载比例δ,通过贪婪的搜索算法求解当前最优的用户-服务器关联策略,通过拉格朗日乘子法结合启发式策略求解计算资源分配,确定本次的用户-服务器关联策略A和计算资源分配F;再次,将A和F返回给改进的分组教学优化算法,并更新B和δ。重复上述过程,循环迭代直至满足算法结束条件,得到最优的调度结果。

译

4.1 计算资源分配策略

通过观察可知,约束式(12f)、式(12g)与其他约束是相互解耦的,通过先固定用户-边缘服务器关联决策A、任务执行位置决策B和任务卸载比例δ,将原问题转化为

译

\{\begin{array}{l} \underset{A, B, δ}{m i n} T^{*} (A, B, δ), \\ s . t . (12 a) - (12 e) 。 \end{array}

(13)

将式(13)展开,得到

译

\underset{A, B, δ}{m i n}

T^*(A,B,δ)=

\underset{F}{m i n} \sum_{i = 1}^{|N|}

max{

T_{i}^{l}

T_{i}^{o f f}

} 。

(14)

对于本地执行时间大于边缘执行时间的任务,减少计算资源分配来使边缘执行时间等于本地执行时间,冗余的计算资源返回边缘服务器的资源池重新分配。假设第1次分配在边缘服务器j上执行的任务均满足本地执行时间小于边缘执行时间,则使用拉格朗日乘子法求解当前最优计算资源分配,判断本地执行时间和边缘执行时间的关系,将冗余的资源分配给其他任务。循环上述过程,直到不存在冗余资源,求得当前执行位置决策、用户-服务器关联决策和任务卸载比例下最优的计算资源分配。将式(13)的优化问题重新定义为P1.1:

译

P1.1:

\underset{F}{m i n} \sum_{j = 1}^{|M|} \sum_{i \in Φ_{j}}^{} \frac{δ_{i} s_{i}}{f_{i j}^{e}}

(15)

s.t.

f_{i j}^{e}

≥0,∀i∈Φ_j, j∈M,

(15a)

\sum_{i \in Φ_{j}}^{} f_{i j}^{e}

≤F_j, ∀j∈M 。

(15b)

观察可知,约束式(15a)和式(15b)为凸约束,将目标函数定义为

译

χ(F)=

\sum_{j = 1}^{|M|} \sum_{i \in Φ_{j}}^{} \frac{δ_{i} s_{i}}{f_{i j}^{e}}

。

(16)

对χ(F)求取二次导数,得

译

\frac{\partial^{2} χ (F)}{\partial^{2} f_{i j}^{e}}

\frac{2 δ_{i} s_{i}}{(f_{i j}^{e})^{3}}

>0,

(17)

\frac{\partial^{2} χ (F)}{\partial f_{i j}^{e} \partial f_{i' j'}^{e}}

=0,∀(i,j)≠(i',j') 。

(18)

通过式(17)和式(18)可得,函数式(16)的海森矩阵为正定矩阵,χ(F)为凸函数,结合约束条件式(15a)和式(15b),定义拉格朗日函数:

译

L(χ(F),λ)=

\sum_{j = 1}^{|M|} \sum_{i \in Φ_{j}}^{} \frac{δ_{i} s_{i}}{f_{i j}^{e}}

+λ_j

(\sum_{i \in Φ_{j}}^{} f_{i j}^{e} - F_{j})

。

(19)

在最优解F^*处,应满足KKT(Karush-Kuhn-Tucker)条件,得到边缘服务器为每个任务分配的计算资源量 $f_{i j}^{e^{*}}$ 为

译

f_{i j}^{e^{*}}

\frac{F_{j} (δ_{i} s_{i})^{1 / 2}}{\sum_{i \in Φ_{j}}^{} (δ_{i} s_{i})^{1 / 2}}

, ∀j∈M 。

(20)

因此,对本地执行时间大于边缘执行时间的任务重新分配资源,具体操作为:令 $T_{i}^{l}$ = $T_{i}^{o f f}$ ,得到更新应该分配的资源量 $f_{i j}^{e^{*}}$ ,然后将冗余的资源返回到边缘服务器计算资源池,重新进行分配。更新后分配的资源量 $f_{i j}^{e^{*}}$ 表示:

译

f_{i j}^{e^{*}}

\frac{δ_{i} s_{i}}{(1 - δ_{i}) \frac{s_{i}}{f_{i}^{l}} - \frac{δ_{i} u_{i}}{W_{i j} l b (1 + \frac{p_{i} h_{i j}}{N_{0}})} - \sum_{j' = 1}^{|M|} \sum_{k = 1}^{|M|} \sum_{e_{j' k} \in Ω_{i}}^{} \frac{δ_{i} u_{i}}{e_{j k}}}

。

(21)

4.2 用户-边缘服务器关联策略

考虑边缘服务器密集部署的情况,根据用户和边缘服务器的地理位置关系,位于覆盖重叠区域的用户可以接入多台边缘服务器。对于非重叠区域的用户,只能接入1台边缘服务器,其关联决策将不再变化。因此,在制定用户-边缘服务器关联决策时,只需要考虑可接入多台边缘服务器的用户,根据任务卸载时间和转发时间决定关联的边缘服务器。文中采用贪心关联策略,使全局任务上传时间与转发时间的和最小,得到用户-边缘服务器关联策略的次优解。全局任务的通信时间T_R(A)定义为

译

T_R(A)=

\sum_{i = 1}^{|N|} \sum_{j = 1}^{|M|} T_{i}^{u p}

T_{i}^{t r a n s}

。

(22)

T_R(A)中的任务转发时间与边缘服务器间最短路径P_j_,_k关联。假设每个时隙边缘服务器间有线链路带宽不变,且不考虑数据传输的并发性,问题转化为求两点间的最短路问题。最短路问题可以通过Floyd算法实现,在算法的初始化阶段执行一次。文中提出基于最小化全局通信时间用户-边缘服务器关联决策的贪心搜索算法,算法伪代码如算法1所示。

译

算法1 用户-边缘服务器关联决策贪心搜索算法。

译

初始化:用户-边缘服务器A,用户集合U

译

① for每个用户i do

译

② 选择具有最大信道增益的边缘服务器j并设置a_ij=1

译

③ if用户i可以访问1个以上边缘服务器

译

④ 将用户i添加至U

译

⑤ end if

译

⑥ end for

译

⑦ 获得全局最优通信时间T_R(A)

译

⑧ repeat

译

⑨ for对每个用户i∈U do

译

⑩ 选择其他边缘服务器j'(h_ij'>0),设置a_ij=0,a_ij'=1,得到新的决策A'

译

⑪ 获得当前全局最优通信时间T_R(A')

译

⑫ if T_R(A')<T_R(A)

译

⑬ 更新当前用户-边缘服务器关联决策A←A'

译

⑭ end if

译

⑮ end for

译

⑯ 直到A没有更新

译

⑰ 返回最优用户-边缘服务器关联决策A^*

译

算法1中,步骤①~⑥遍历所有用户,将每个用户关联到离自己最近的边缘服务器,得到初始关联策略A。步骤⑦计算当前系统的总通信传输时间T_R(A)。步骤⑧~⑯对用户集合U的用户i找到可更换的边缘服务器j',如果更新后决策的通信传输时间更优,将A更新为A',直至用户-边缘服务器关联决策不再变化。步骤⑰返回最优的用户-边缘服务器关联决策集合。

译

4.3 任务卸载执行位置和卸载比例搜索算法

文中应用改进的分组教学优化算法^[

17]求解任务执行位置和卸载比例联合搜索问题。分组教学优化算法是一种模拟群体教学体制的元启发式优化算法,其算法灵感来自于小组教学机制^{[参考文献 18

百度学术

18]}。首先根据特定的规则将学生们分为几组,然后结合每个小组的特点,运用具体的教学方法提高小组知识水平。文中根据以下定义的4条规则,构建一个通用的分组教学模型:

译

(1) 学生之间接受知识的能力存在差异,差异越大,教师在制定教学计划时面临的挑战越大。

译

(2) 一个好的教师更关注接受知识能力较差的学生,而不是接受知识能力强的学生。

译

(3) 在课余时间,学生可以通过自学和与其他学生交流来获得知识。

译

(4) 良好的教师分配机制对提高学生知识水平有很大帮助。

译

然而每个学生在学生阶段都有相同的学习方式,但每个学生有不同的学习动机,优秀的学生具有较强的自学能力,普通学生自主学习动机一般,需要老师和其他同学的帮助。针对此问题,通过加入学习动机,使精英学生自主学习,而普通学生会相互交流提高综合能力,并加入了随机的反向学习策略,提高算法优化性能。将上述改进思路应用于分组教学优化算法,并与文中所提出的边缘协作环境下任务部分卸载与调度模型适配。分组教学优化算法的基本流程如图1所示。

译

图1 分组教学优化算法的基本流程

下载: 原图 | 高精图 | 低精图

(1) 编码与解码。假设班级学生集合为P,每个学生的知识算子z_p=( $z_{p, 1}^{i}$ , $z_{p, 2}^{i}$ )定义为二维变量,对应卸载执行位置决策B和卸载比例δ。根据约束式(12b)和式(12d),任务的执行位置只有一个,将执行位置决策变量编码为一维变量 $z_{p, 1}^{i}$ =j,∀j∈M,卸载比例 $z_{p, 2}^{i}$ ∈[0,1],∀i∈N。当 $z_{p, 2}^{i}$ =0或j=0时,表示任务完全在本地执行。

译

(2) 适应度函数设计。在任务卸载场景下解码得到当前卸载执行位置决策B_p和任务卸载比例δ_p,通过计算资源分配策略和用户-边缘服务器关联策略,求得用户-边缘服务器关联决策A_p和最优计算资源分配F_p,求得任务执行时间。将适应度函数表示为

译

f(z_p,A_p,F_p)=

\sum_{i = 1}^{|N|}

max{

T_{i}^{l}

T_{i}^{o f f}

} 。

(23)

(3) 初始化。将初始的|P|-1个学生都根据任务执行位置B和任务卸载比例δ的定义域随机选取可行解,对班级的最后一个学生,应用关联最近边缘服务器的二进制非协作卸载策略进行初始化。具体流程为:使所有卸载比例为1,表示二进制卸载;根据用户-边缘服务器的信道增益,用户选择信道增益最大的边缘服务器关联;所有用户-边缘服务器关联策略和任务卸载执行位置决策相同,不需要边缘协作转发,求解计算资源分配。应用上述策略得到一组贪心的可行解作为初始解,进入迭代搜索流程。

译

(4) 能力分组阶段。为了更好地展示分组教学的优势,所有学生会根据自己的知识水平分为两组,强大的一组被称为精英学生,另一组为普通学生。在教学时老师根据不同的组制定不同的教学计划,在一个学习周期后再次进行分组。

译

(5) 更新教师和班级平均知识。模仿灰狼优化中的保留3个最优解的思想,根据适应度函数f(z_p,A_p,F_p)求得当前班级内前三的学生成绩,教师分配机制可表示为

译

$z_{\text {teacher }}=\left\{

\begin{array}{l} z_{first}, f (z_{first}, A_{first}, F_{first}) ⩽ f (z_{avg}, A_{avg}, F_{avg}), \\ z_{avg}, f (z_{first}, A_{first}, F_{first}) > f (z_{avg}, A_{avg}, F_{avg}), \end{array}

\right.$

(24)

其中,z_first、z_second和z_third分别为第1优、第2优和第3优学生;z_zvg= $\frac{z_{f i r s t} + z_{s e c o n d} + z_{t h i r d}}{3}$ ,精英组和普通组共用相同的老师。同时求得所有学生的平均知识水平z_mean= $\sum_{p \in P}^{} z_{p}^{i} /$ |P|。

译

(6) 教师阶段Ⅰ。由于精英组接受知识的能力较强,教师更加注重对精英组整体知识的提高,以此尽可能地提高全班平均知识。因此,精英组每个学生向教师学习产生的新的知识为z_newp,可定义为

译

z_newp=z_p+φ₁(z_teacher-φ_TF(φ₂z_mean+φ₃z_p)),

(25)

其中,φ₁、φ₂和φ₃为(0,1)之间的随机数,并且φ₂+φ₃=1,φ_TF随机取1或2。

译

(7) 教师阶段Ⅱ。考虑普通组接受知识能力较差,教师更倾向于从个体角度提高学生的知识水平。因此,普通组通过以下方式获取知识:

译

z_newp=z_p+2φ₄(z_teacher-z_p),

(26)

其中,φ₄为(0,1)之间的随机数。

译

根据式(23)求适应度函数值f(z_newp,A_newp,F_newp),当f(z_newp,A_newp,F_newp)<f(z_p,A_p,F_p)时,新解将替换原解,否则原解不变。

译

(8) 学生阶段Ⅰ。在原始算法的学生阶段,每个学生可以通过自学或与其他同学交流来获得知识。然而,精英学生比普通学生具有更强的学习能力和动力,更倾向于自学。因此,精英学生根据

译

\frac{(1 - p)}{|P| s i n (2 π r)}

(27)

获得学习动机,并通过下式获得新解:

译

z_newp=z_p+Dz_p 。

(28)

(9) 学生阶段Ⅱ。普通学生的学习能力较弱,往往在同学之间互相学习。因此,普通组学生互相学习阶段学生p₁随机选择另一位学生p₂产生新解 $z_{n e w p_{1}}$ 的公式定义为

译

$z_{\text {nevpl }}=\left\{

\begin{array}{l} z_{p 1} + φ_{5} (z_{p 1} - z_{p 2}), f (z_{p_{1}}, A_{p_{1}}, F_{p_{1}}) < f (z_{p_{2}}, A_{p_{2}}, F_{p_{2}}) \\ z_{p 1} + φ_{5} (z_{p 2} - z_{p 1}), f (z_{p_{1}}, A_{p_{1}}, F_{p_{1}}) ⩾ f (z_{p_{2}}, A_{p_{2}}, F_{p_{2}}) \end{array}

\right.$

(29)

其中,φ₅表示(0,1)之间的随机数。

译

(10) 随机反向学习。反向学习策略能够根据当前解获取一个反向解,在此基础上增加(0,1)的随机值,使算法有更强的搜索能力和收敛能力。产生新解的具体公式如下:

译

z_newp=u_b+l_b-rz_p,

(30)

其中,r为(0,1)之间的随机数。

译

如果随机反向学习后新解更优,则替换原始解。至此,一轮IGTOA算法迭代过程结束,此后循环迭代直到收敛。基于改进教学优化算法的任务调度算法描述如算法2所示。

译

算法2 改进分组教学优化算法。

译

① 初始化:通过Floyd算法得到边缘服务器之间的最优传输路径,通过贪心算法得到P-1个学生的初始决策,初始化迭代数量g=1

译

② while g≤I do

译

③ 根据式(24)更新z_teacher和z_mean

译

④ 将所有学生分为精英学生S_good和普通学生S_bad

译

⑤ for p=1 to|P| do

译

⑥ if学生为精英学生S_good

译

⑦ 根据式(25)实行教学阶段

译

⑧ 学生根据式(27)得到学习动机并根据式(28)执行学生阶段

译

⑨ end if

译

⑩ if学生为普通学生S_bad

译

⑪ 根据式(26)执行教学阶段

译

⑫ 根据式(29)执行学生阶段

译

⑬ end if

译

⑭ 根据算法1和式(21)获得A和F

译

⑮ if f(z_newp,A_newp,F_newp)<f(z_p,A_p,F_p) 更新z_p←z_newp

译

⑯ 根据式(30)执行随机反向学习阶段

译

⑰ if f(z_newp,A_newp,F_newp)<f(z_p,A_p,F_p) 更新z_p←z_newp

译

⑱ 更新z_teacher和z_mean

译

⑲ end for

译

⑳ g←g+1

译

㉑ end while

译

㉒返回最优调度决策A^*,B^*,δ^*,F^*

译

步骤①首先通过Floyd算法求解边缘服务器之间的最短传输路径Path,根据贪心初始化策略得到班级初始的知识,初始化迭代次数为1;步骤③得到当前班级教师以及所有学生的平均知识水平;步骤④将班级学生划分为精英组和普通组;步骤⑦~⑭对精英组和普通组学生开展不同的教师教学阶段和学生学习阶段,如果新解优于旧解,则替换旧解;步骤⑮~⑯使用随机反向学习策略生成反向解,如果新解更优,则替换旧解。此后更新教师和班级平均知识,本轮迭代结束。如果此时到达最大迭代次数,则返回当前最优的任务调度决策;否则,返回步骤②,开始新一轮的搜索操作;步骤㉒返回最优调度决策。

译

4.4 算法复杂度分析

文中提出的基于改进分组教学优化算法的任务调度策略主要可分为初始化阶段、能力分组阶段、教师教学阶段、学生学习阶段和随机反向学习阶段,其中教师教学阶段和学生学习阶段都应用计算资源分配策略和算法1。其中,|N|表示用户设备数量,|M|表示服务器数量。每个阶段的时间复杂度分析如下:初始化阶段,应用Floyd算法求解|M|台服务器之间的最短传输路径集合,时间复杂度为O(|M|³)。设学生数量为|P|,最大循环次数为I,在改进的分组教学优化算法的任务调度策略的每次内层循环中,随机反向学习阶段时间复杂度为O(|N|)。计算资源分配策略时间复杂度为O(|N|²),算法1的时间复杂度为O(|N|×|M|),教师教学阶段和学生学习阶段的时间复杂度为O(|N|+|N|²+|N|×|M|)。由于文中在实验过程中,将服务器的数量|M|设置为常数,并远小于循环次数和用户设备数量,同时,文中假设调度过程基于准静态场景,Floyd算法只在初始化阶段运行一次,初始化时间相比迭代求解的时间可忽略不计。综上所述,算法2的时间复杂度为O(I×|P|×|N|²)。

译

5 实验结果与分析

使用Java编写仿真环境,参考文献[

16,19]的参数设置和网络拓扑设置进行模拟实验。基础仿真环境考虑9个边缘服务器分布在1 500 m×1 500 m的范围内,相邻边缘服务器之间的距离为300 m,边缘服务器之间有线链路的带宽为500 Mb/s,每个边缘服务器的覆盖半径为200 m,用户随机分布在边缘服务器的覆盖范围内。实验对比的指标定义如下。

译

(1) 任务平均执行时间。由于系统任务执行时间与用户数量线性相关,为将数据表示统一,在实验结果分析时使用任务平均执行时间 $\bar{T}$ 来评估实验结果,定义如下:

译

\bar{T}

\sum_{i = 1}^{|N|} T_{i} /

|N| 。

(31)

(2) 服务器j上执行的任务总量为O(j)。该指标评估不同策略下用户卸载执行的任务量之和,也可以评估某个服务器j上负载与服务器计算能力是否匹配。服务器j上执行的任务总量可表示为

译

O(j)=

\sum_{i = 1}^{|N|}

b_ijδ_is_i 。

(32)

(3) 其他的仿真参数设置如表1所示。

译

表1 仿真参数

参数	值
用户数量	20~120
边缘服务器数量	9
路径损失因子	4
边缘服务器无线信号覆盖半径/m	200
信道背景噪声功率/dBm	-100
用户设备上传功率/mW	100
边缘服务器通信带宽/MHz	[10,50]
用户设备本地计算能力/GHz	1
边缘服务器计算能力/GHz	[20,60]
边缘服务器间有线链路带宽/(Mb·s^-1)	500
任务输入数据大小/MB	[0.5,50]
任务所需计算量大小/GHz	[1,10]

下载: CSV

为了验证文中提出的基于改进分组教学优化算法的任务调度算法IGTOA的有效性,将其与以下算法对比:

译

(1) GTOA^[

18]。原始分组教学优化算法,没有给学生添加学习动机,并且缺少了随机反向学习策略来扩大搜索范围。

译

(2) ACS^[

20]。计算资源分配为固定策略,每个边缘服务器根据在该边缘服务器上执行的任务个数平均分配计算资源,根据本地执行时间等于边缘执行时间的关系确定卸载比例。

译

(3) DTPSO^[

21]。使用离散三元粒子群算法求解终端设备协作的任务卸载和资源分配问题,将其改造为求解边缘协作场景下任务卸载和资源分配的算法。

译

(4) HJTORA^[

22]。结合启发式和凸优化理论的任务卸载与资源调度算法,卸载方式为二进制卸载,结合文中提出的边缘-边缘协作框架,将原始的HJTORA算法改造为可以协作的算法。

译

首先验证所提出算法的收敛性和有效性。将原始的GTOA算法、基于粒子群算法改进的用于处理离散型问题的DTPSO算法以及文中提出的IGTOA算法进行对比。用户数量分别设置为40和100,各个算法的适应度函数值如图2所示。对比基础的GTOA算法以及DTPSO算法,可以观察到IGTOA算法收敛速度较快,原始的GTOA算法有较强的局部搜索能力,在算法执行的前期能够快速收敛。文中结合随机反向学习策略获得反向解范围内的随机解,能够扩大搜索范围,增强种群多样性,避免陷入局部最优解。此外,文中为精英组学生添加了学习动机,使精英学生能够通过自学来提高自身知识水平,来尽可能地获得最优解。IGTOA在原始算法的基础上增加了这些改进,在搜索最优解的能力和收敛速度上均有所提升。

译

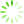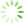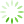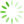
图2 不同算法适应度函数值的变化

下载: 原图 | 高精图 | 低精图

实验2验证在用户均匀分布、边缘服务器性能异构场景下算法的有效性。边缘服务器的计算能力为3种类型:类型1为20 GHz,类型2为40 GHz,类型3为60 GHz,每种类型的边缘服务器数量相同。用户数量对任务执行时间和每种类型边缘服务器任务量大小的影响如图3所示。在相同的用户分布下,由于边缘服务器的异构性,可能加重边缘侧负载不均衡的情况,IGTOA算法相比ACS算法,用户平均执行时间降低约5%~10%,相比HJTORA算法降低约23%~35%,且随着用户数量的增加,执行时间降低的幅度增大。文中提出的基于边缘协作架构的算法能够协调工作负载,将计算量大的任务转发到性能高的邻近边缘服务器,计算量小的任务转发到性能较差的边缘服务器,3种类型边缘服务器的工作负载总量在用户数量较少的时候,比例达到1∶2∶4,随着用户数量增大近似满足1∶2∶3的比例。

译

图3 边缘服务器异构、用户分布均匀时用户数量的影响

下载: 原图 | 高精图 | 低精图

文中的边缘协作框架能够缓解由于边缘服务器异构性、任务大小差异性带来的全局负载不均衡的影响,接下来通过实验验证用户分布不均匀的影响。在生成用户时,将用户集中在一些边缘服务器上,使初始负载不均衡,实验设置将50%的用户初始位置用户集中在热点边缘服务器,50%用户随机分布在区域内其他边缘服务器的覆盖范围,在这样的用户分布场景下,任务平均执行时间随用户数量的变化趋势如图4所示。

译

图4 边缘服务器异构、用户分布不均匀时用户数量的影响

下载: 原图 | 高精图 | 低精图

在用户分布不均匀的场景下,当用户数量增大时,用户集中区域的边缘服务器将过载,导致分配给用户的计算资源减少。IGTOA算法能够根据全局资源视图搜索潜在的可应用的边缘服务器,并将任务转发到非本地接入的边缘服务器上,平均执行时间相比不考虑边缘协作的ACS降低约10%~15%;相比二进制卸载算法HJTORA降低约30%~60%。结合上述结果,与文中的模型分析可知:由于用户分布不均匀以及部分边缘服务器资源不足,不考虑协作会导致大量用户任务等待和分配到的资源减少。此时,边缘服务器之间协作卸载可以发挥优势。然而,随着用户数量的增加,性能优化的比例逐渐减少。原因是:边缘服务器的计算资源是有限的,用户数量增加导致资源的竞争使每个用户能分配到的计算资源减少,进而边缘协作的性能会随着用户数量的增大而降低,表现为图中执行时间降低比例的缩小。

译

6 结束语

文中针对移动边缘计算中由于用户地理位置分布不均而造成边缘服务器资源无法充分利用的问题,对边缘服务器协作方式与任务卸载方式进行研究和归纳总结,以最小化任务完工时间为目标,构建了边缘协作环境下的任务部分卸载与调度模型,提出了一种基于改进分组教学优化算法的任务调度算法。首先,根据用户和边缘服务器的位置关系以及边缘服务器的网络拓扑,以最小化任务完工时间为目标,建立边缘协作环境下的任务部分卸载与调度模型;其次,为解决计算资源分配、用户-边缘服务器关联决策、任务卸载比例以及任务执行位置决策多变量耦合的联合优化问题,文中使用子问题分解方式降低求解难度,结合拉格朗日乘子法、贪心思想求解计算资源分配子问题和用户-边缘服务器关联子问题,进而为求解任务执行位置和卸载比例,通过优化了种群的初始化,结合选择、变异、精英替换策略,提出了改进的分组教学优化算法;最后,对上述子问题交替迭代求解,得到最优的调度决策。实验证明,文中所提算法在边缘协作环境下能有效降低任务完工时间,并具有较好的收敛性。在未来的研究中,希望考虑边缘服务器聚类与部署位置,来提高边缘侧服务性能,减少部署经济成本,并借助车辆或无人机等中继节点来解决无线通信范围受限的问题。

译

参考文献

[1]

LIANG Y, WANG W, ZHENG X, et al. Collaborative Edge Service Placement for Maximizing QoS with Distributed Data Cleaning[C]//2023 IEEE/ACM 31st International Symposium on Quality of Service(IWQoS).Piscataway:IEEE, 2023: 1-4. [百度学术]

[2]

宋宇波, 金星妤, 燕锋, 等. 车联网中移动边缘计算的安全高效节能卸载策略[J]. 清华大学学报(自然科学版), 2021, 61(11):1246-1253. [百度学术]

SONG Yubo, JING Xingyu, YAN Feng, et al. Secure and Energy Efficient Offloading of Mobile Edge Computing in the Internet of Vehicles[J]. Journal of Tsinghua University(Science and Technology), 2021, 61(11):1246-1253. [百度学术]

[3]

YUAN H, ZHOU M C. Profit-Maximized Collaborative Computation Offloading and Resource Allocation in Distributed Cloud and Edge Computing Systems[J]. IEEE Transactions on Automation Science and Engineering, 2020, 18(3):1277-1287. [百度学术]

[4]

DING Y, LI K, LIU C, et al. A Potential Game Theoretic Approach to Computation Offloading Strategy Optimization in End-Edge-Cloud Computing[J]. IEEE Transactions on Parallel and Distributed Systems, 2021, 33(6):1503-1519. [百度学术]

[5]

ZHOU T, YUE Y, QIN D, et al. Joint Device Association,Resource Allocation,and Computation Offloading in Ultradense Multidevice and Multitask IoT Networks[J]. IEEE Internet of Things Journal, 2022, 9(19):18695-18709. [百度学术]

[6]

赵辉, 冯南之, 王泉, 等. 面向边缘计算平台的半线上任务动态调度方法[J]. 西安电子科技大学学报, 2021, 48(6):8-15. [百度学术]

ZHAO Hui, FENG Nanzhi, WANG Quan, et al. Dynamic Semi-Online Task Scheduling Method for the Edge Computing Platform[J]. Journal of Xidian University, 2021, 48(6):8-15. [百度学术]

[7]

彭青蓝, 夏云霓, 郑万波, 等. 一种去中心化的在线边缘任务调度与资源分配方法[J]. 计算机学报, 2022, 45(7):1462-1477. [百度学术]

PENG Qinglan, XIA Yunni, ZHENG Wanbo, et al. A Decentralized Approach to Online Edge Task Scheduling and Resource Allocation[J]. Journal of Computer Science, 2022, 45(7):1462-1477. [百度学术]

[8]

WANG K, CHEN W, LI J, et al. Joint Task Offloading and Caching for Massive MIMO-Aided Multi-Tier Computing Networks[J]. IEEE Transactions on Communications, 2022, 70(3):1820-1833. [百度学术]

[9]

邝祝芳, 陈清林, 李林峰, 等. 基于深度强化学习的多用户边缘计算任务卸载调度与资源分配算法[J]. 计算机学报, 2022, 45(4):812-824. [百度学术]

KUANG Zhufang, CHEN Qinglin, LI Linfeng, et al. Task Offloading Scheduling and Resource Allocation Algorithm for Multi-User Edge Computing Based on Deep Reinforcement Learning[J]. Journal of Computer Science, 2022, 45(4):812-824. [百度学术]

[10]

NING Z, DONG P, WANG X, et al. Partial Computation Offloading and Adaptive Task Scheduling for 5G-Enabled Vehicular Networks[J]. IEEE Transactions on Mobile Computing, 2020, 21(4):1319-1333. [百度学术]

[11]

MALIK R, VU M. On-Request Wireless Charging and Partial Computation Offloading in Multi-Access Edge Computing Systems[J]. IEEE Transactions on Wireless Communications, 2021, 20(10):6665-6679. [百度学术]

[12]

ZHANG W, ZHANG Z, ZEADALLY S, et al. Energy-Efficient Workload Allocation and Computation Resource Configuration in Distributed Cloud/Edge Computing Systems with Stochastic Workloads[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(6):1118-1132. [百度学术]

[13]

HU S, LI G. Dynamic Request Scheduling Optimization in Mobile Edge Computing for IoT Applications[J]. IEEE Internet of Things Journal, 2020, 7(2):1426-1437. [百度学术]

[14]

ELGENDY I A, ZHANG W Z, HE H, et al. Joint Computation Offloading and Task Caching for Multi-User and Multi-Task MEC Systems:Reinforcement Learning-Based Algorithms[J]. Wireless Networks, 2021, 27(3):2023-2038. [百度学术]

[15]

LIU X, YU J, WANG J, et al. Resource Allocation with Edge Computing in IoT Networks via Machine Learning[J]. IEEE Internet of Things Journal, 2020, 7(4):3415-3426. [百度学术]

[16]

LIU X, ZHAO X, LIU G, et al. Collaborative Task Offloading and Service Caching Strategy for Mobile Edge Computing[J]. Sensors, 2022, 22(18):6760. [百度学术]

[17]

RAO H, JIA H, WU D, et al. A Modified Group Teaching Optimization Algorithm for Solving Constrained Engineering Optimization Problems[J]. Mathematics, 2022, 10(20):3765. [百度学术]

[18]

ZHANG Y, JIN Z. Group Teaching Optimization Algorithm:A Novel Metaheuristic Method for Solving Global Optimization Problems[J]. Expert Systems with Applications, 2020,148:113246-113264. [百度学术]

[19]

GUO F, ZHANG H, JI H, et al. An Efficient Computation Offloading Management Scheme in the Densely Deployed Small Cell Networks with Mobile Edge Computing[J]. IEEE/ACM Transactions on Networking, 2018, 26(6):2651-2664. [百度学术]

[20]

MAHMOOD A, HONG Y, EHSAN M K, et al. Optimal Resource Allocation and Task Segmentation in IoT Enabled Mobile Edge Cloud[J]. IEEE Transactions on Vehicular Technology, 2021, 70(12):13294-13303. [百度学术]

[21]

LIU Z, FAN J, GENG S, et al. Joint Optimization of Task Offloading and Computing Resource Allocation in MEC-D2D Network[C]//2022 IEEE 5th International Conference on Computer and Communication Engineering Technology(CCET).Piscataway:IEEE, 2022: 256-260. [百度学术]

[22]

TRAN T X, POMPILI D. Joint Task Offloading and Resource Allocation for Multi-Server Mobile-Edge Computing Networks[J]. IEEE Transactions on Vehicular Technology, 2018, 68(1):856-868. [百度学术]

摘要

由于用户地理位置分布不均可能导致边缘服务器负载不均衡

难以为用户提供满意的服务质量。此外

边缘服务器可用资源有限

一些大任务可能难以全部卸载到边缘服务器。针对以上问题

利用多个边缘服务器之间的协作

结合任务部分卸载方式

提出一种边缘协作环境下最小化完工时间的任务调度方法。首先

结合边缘水平协作和任务部分卸载技术

考虑多用户多边缘服务器场景下用户和边缘服务器的位置关系

以最小化任务完工时间为目标

建立任务部分卸载调度模型;其次

提出基于改进分组教学优化算法的任务调度算法

联合优化边缘服务器计算资源分配、用户-边缘服务器关联决策、任务卸载比例以及执行位置决策

以最小化任务完工时间为目标

实现边缘计算环境下任务的高效调度;最后

通过实验将提出的任务调度算法与其他算法在多个指标下进行对比。实验结果表明

所提方法能够有效降低任务完工时间。

Abstract

The uneven geographical distribution of users may lead to unbalanced load on edge servers

which makes it difficult to provide satisfactory service quality for users.In addition

the available resources of the edge server are limited

and some large tasks may be difficult to offload to the edge server.To solve the above problems

this paper proposes a task scheduling method to minimize the completion time in the edge collaboration environment by utilizing the collaboration among multiple edge servers and combining the task partial offloading technology.First

by combining the edge of horizontal collaboration and task partial offloading technology and considering the position relationship between users and edge servers in multi-user multi-edge server scenario

a task partial offloading and scheduling model is established to minimize the task completion time.Second

a task scheduling algorithm based on the Improved Group Teaching Optimization Algorithm(IGTOA) is proposed to jointly optimize the edge server computing resource allocation

user-edge server association decision

task offloading ratio and execution location decision.With minimizing the task completion time as the goal

efficient task scheduling is achieved under edge computing environment.Finally

the proposed task scheduling algorithm is compared with DTOSO

HJTORA and ACS algorithms under multiple indexes.Experimental results show that the proposed method can effectively reduce the task completion time.

关键词

边缘协作部分卸载调度算法分组教学优化算法

Keywords

edge collaborationpartial offloadingscheduling algorithmgroup teaching optimization algorithm

references

宋宇波, 金星妤, 燕锋, 等. 车联网中移动边缘计算的安全高效节能卸载策略[J]. 清华大学学报(自然科学版), 2021, 61(11):1246-1253.

赵辉, 冯南之, 王泉, 等. 面向边缘计算平台的半线上任务动态调度方法[J]. 西安电子科技大学学报, 2021, 48(6):8-15.

ZHAO Hui, FENG Nanzhi, WANG Quan, et al. Dynamic Semi-Online Task Scheduling Method for the Edge Computing Platform[J]. Journal of Xidian University, 2021, 48(6):8-15.

彭青蓝, 夏云霓, 郑万波, 等. 一种去中心化的在线边缘任务调度与资源分配方法[J]. 计算机学报, 2022, 45(7):1462-1477.

PENG Qinglan, XIA Yunni, ZHENG Wanbo, et al. A Decentralized Approach to Online Edge Task Scheduling and Resource Allocation[J]. Journal of Computer Science, 2022, 45(7):1462-1477.

WANG K, CHEN W, LI J, et al. Joint Task Offloading and Caching for Massive MIMO-Aided Multi-Tier Computing Networks[J]. IEEE Transactions on Communications, 2022, 70(3):1820-1833.

邝祝芳, 陈清林, 李林峰, 等. 基于深度强化学习的多用户边缘计算任务卸载调度与资源分配算法[J]. 计算机学报, 2022, 45(4):812-824.

NING Z, DONG P, WANG X, et al. Partial Computation Offloading and Adaptive Task Scheduling for 5G-Enabled Vehicular Networks[J]. IEEE Transactions on Mobile Computing, 2020, 21(4):1319-1333.

MALIK R, VU M. On-Request Wireless Charging and Partial Computation Offloading in Multi-Access Edge Computing Systems[J]. IEEE Transactions on Wireless Communications, 2021, 20(10):6665-6679.

HU S, LI G. Dynamic Request Scheduling Optimization in Mobile Edge Computing for IoT Applications[J]. IEEE Internet of Things Journal, 2020, 7(2):1426-1437.

LIU X, YU J, WANG J, et al. Resource Allocation with Edge Computing in IoT Networks via Machine Learning[J]. IEEE Internet of Things Journal, 2020, 7(4):3415-3426.

LIU X, ZHAO X, LIU G, et al. Collaborative Task Offloading and Service Caching Strategy for Mobile Edge Computing[J]. Sensors, 2022, 22(18):6760.

RAO H, JIA H, WU D, et al. A Modified Group Teaching Optimization Algorithm for Solving Constrained Engineering Optimization Problems[J]. Mathematics, 2022, 10(20):3765.

ZHANG Y, JIN Z. Group Teaching Optimization Algorithm:A Novel Metaheuristic Method for Solving Global Optimization Problems[J]. Expert Systems with Applications, 2020,148:113246-113264.

MAHMOOD A, HONG Y, EHSAN M K, et al. Optimal Resource Allocation and Task Segmentation in IoT Enabled Mobile Edge Cloud[J]. IEEE Transactions on Vehicular Technology, 2021, 70(12):13294-13303.

TRAN T X, POMPILI D. Joint Task Offloading and Resource Allocation for Multi-Server Mobile-Edge Computing Networks[J]. IEEE Transactions on Vehicular Technology, 2018, 68(1):856-868.

浏览量

下载量

CSCD

文章被引用时，请邮件提醒。

提交

工具集

关联资源

一种新的输入缓存Clos结构及其路由/调度算法

L-模糊集信任机制的网格计算任务调度方法