双向长短期记忆网络的时间序列预测方法

管业鹏; 苏光耀; 盛怡

doi:10.19665/j.issn1001-2400.20231205

English Version

您当前的位置：

首页 >

文章列表页 >

双向长短期记忆网络的时间序列预测方法

信息与通信工程 | 更新时间：2024-07-23

- 双向长短期记忆网络的时间序列预测方法
- Time series prediction method based on the bidirectional long short-term memory network
- 角色： First author , 第一作者 ,
  
  机构：
  上海大学通信与信息工程学院,上海 200444
  
  邮箱： shugyp@yeah.net
  
  简介： [ "管业鹏(1967—),男,教授,E-mail:shugyp@yeah.net" ]
  
  暂无本作者相关信息
  管业鹏
  1 ，
  角色：
  
  机构：
  上海大学通信与信息工程学院,上海 200444
  
  邮箱： 13235373474@163.com
  
  简介： [ "苏光耀(2000—),男,上海大学硕士研究生,E-mail:13235373474@163.com" ]
  
  暂无本作者相关信息
  苏光耀
  1 ，
  角色： Corresponding author , 通讯作者 ,
  
  机构：
  上海体育学院竞技运动学院,上海 200438
  
  邮箱： 549316264@qq.com
  
  简介：盛怡(1981—),女,副教授,E-mail:549316264@qq.com
  
  暂无本作者相关信息
  盛怡
  2 ，
- 西安电子科技大学学报 2024年51卷第3期页码：103-112
- 作者机构：
  
  1. 上海大学通信与信息工程学院,上海 200444
  2. 上海体育学院竞技运动学院,上海 200438
- 作者简介：
  
  [ "管业鹏(1967—),男,教授,E-mail:shugyp@yeah.net" ]
  [ "苏光耀(2000—),男,上海大学硕士研究生,E-mail:13235373474@163.com" ]
  盛怡(1981—),女,副教授,E-mail:549316264@qq.com
- 基金信息：
  
  国家重点研发计划(2019YFC1520500)
- DOI：10.19665/j.issn1001-2400.20231205
  中图分类号： TP391.41
- 纸质出版日期：2024-06-20，
  
  网络出版日期：2023-12-27，
  
  收稿日期：2023-07-26，
- 稿件说明：
扫描看全文
引用本文

阅读全文PDF
管业鹏, 苏光耀, 盛怡. 双向长短期记忆网络的时间序列预测方法[J]. 西安电子科技大学学报, 2024,51(3):103-112.

Yepeng GUAN, Guangyao SU, Yi SHENG. Time series prediction method based on the bidirectional long short-term memory network[J]. Journal of Xidian University, 2024,51(3):103-112.
管业鹏, 苏光耀, 盛怡. 双向长短期记忆网络的时间序列预测方法[J]. 西安电子科技大学学报, 2024,51(3):103-112. DOI： 10.19665/j.issn1001-2400.20231205.

Yepeng GUAN, Guangyao SU, Yi SHENG. Time series prediction method based on the bidirectional long short-term memory network[J]. Journal of Xidian University, 2024,51(3):103-112. DOI： 10.19665/j.issn1001-2400.20231205.

摘要

时间序列预测即利用历史时间序列数据,预测未来一段时间内的数据信息,以便提前制定相应策略。目前,时间序列的类别复杂繁多,而现有的时间序列预测模型面对多种类型数据时无法取得稳定预测的结果,进而难以同时满足对现实中多种复杂的时序数据预测的应用需求。针对上述问题,提出了一种基于时间注意力机制双向长短期记忆网络的时间序列预测方法。笔者提出的网络模型采用改进的正向和反向传播机制提取时序信息并通过自适应权重分配策略推理未来的时序信息。具体来说,设计了一个改进的双向长短期记忆网络,通过结合双向长短期记忆和长短期记忆网络提取深度时间序列特征,挖掘上下文的时序依赖关系。在此基础上,融合所提出的时间注意力机制,实现对深度时间序列特征进行自适应加权,提升深度时序特征的显著性表达能力。通过与同类代表性方法在多个不同类别数据集上的客观定量对比,实验结果表明,该方法能够在多种类别的复杂时间序列数据上更优的预测性能。

译

Abstract

Time series prediction means the use of historical time series to predict a period of time in the future,so as to formulate corresponding strategies in advance.At present,the categories of time series are complex and diverse.However,existing time series prediction models cannot achieve stable prediction results when faced with multiple types of time series data.The application requirements of complex time series data prediction in reality are difficult to simultaneously meet.To address the problem,a time series prediction method is proposed based on the Bidirectional Long and Short-term Memory(BLSTM) with the attention mechanism.The improved forward and backward propagation mechanisms are used to extract temporal information.The future temporal information is inferred through an adaptive weight allocation strategy.Specifically,an improved BLSTM is proposed to extract deep time series features and explore temporal dependencies of context by combining BLSTM and Long Short-term Memory(LSTM) networks,on the basis of which the proposed temporal attention mechanism is fused to achieve adaptive weighting of deep time series features,which improves the saliency expression ability of deep time series features.Experimental results demonstrate that the proposed method has a superior prediction performance in comparison with some representative methods in multiple time series datasets of different categories.

译

关键词

时间序列; 双向长短期记忆网络; 长短期记忆网络; 注意力机制; 深度学习

译

Keywords

time series; Bidirectional Long Short-Term Memory; Long Short-Term Memory; attention mechanism; deep learning

译

1 引言

随着大数据时代的到来,复杂时序数据的数量呈指数级增长^[

1]。目前,利用已有历史时间序列数据预测未来时序信息,已在工业、医学及经济等领域得到了广泛应用^{[参考文献 2

百度学术

2参考文献 ⇓

百度学术

⇓参考文献 ⇓

百度学术

⇓参考文献 ⇓-6

⇓-6]}。目前,时间序列的类别复杂繁多,如多元变量和单元变量、长时间序列和短时间序列等。而现有的时间序列预测模型面对多种类型数据时,无法取得稳定预测的结果,难以同时满足对现实中多种复杂的时序数据预测的应用需求。

译

针对时间序列的预测,国内外学者已开展了大量研究。最早,YULE^[

7]依照前后数据的相关性提出了自回归模型(Auto Regressive model,AR)以历史观测数据预测一年中太阳黑子数,但AR模型对数据平稳性要求很高且易受噪声的干扰。为了消除预测中的噪声对AR模型的影响,WALKER^{[参考文献 8

百度学术

8]}提出了通过组合残差项对序列长期趋势预测的移动平均模型(Moving Average model,MA)。随后,多种基于机器学习预测模型被提出,如目前常用的LightGBM^{[参考文献 9

百度学术

9]}和XGBoost^{[参考文献 10

百度学术

10]}等方法。上述方法虽取得了一定的预测效果,但对多变量协同复杂时间序列的预测性能并不理想,因此,这些方法并不适用于目前大多数时序数据的预测。

译

近年来,随着深度学习方法在各领域取得的成功应用,基于深度学习的时间序列预测方法得到了广泛重视。早期,MEDSKER等^[

11]提出了一种基于循环神经网络(Recurrent Neural Network,RNN)模型的时间序列预测方法,但由于RNN存在梯度消失和梯度爆炸等问题,使得该模型训练时难以收敛。HOCHREITER等^{[参考文献 12

百度学术

12]}提出了一种长短期记忆(Long Short-Term Memory,LSTM)模型时间序列预测方法,通过添加遗忘机制解决RNN训练难以收敛问题。但在LSTM网络模型中,数据信息仅能正向传递。而时间序列预测不仅和前期的时序数据信息相关,且与后期的时序数据信息也存在密切关联。因此,HAFEZI等^{[参考文献 13

百度学术

13]}提出了一种基于双向长短期记忆(Bidirectional Long Short-Term Memory,BLSTM)模型的时间序列预测方法。BLSTM模型虽然可兼顾前后时间信息,但由于时间序列各时刻提取到的特征与当前预测值的关联程度不同,直接将正向和反向LSTM提取到的特征信息拼接作为预测结果,使BLSTM对所有信息的重视程度相同,从而易导致预测结果出现偏差。

译

随后,KAUSHIK等^[

14]提出了一种基于BLSTM-L模型的时间序列预测方法,将BLSTM提取到的信息输入到LSTM再次进行时序信息的处理以改善预测效果,但基于循环神经网络的方法在处理长期时序任务时仍不能取得较好的效果。VSWANI等^{[参考文献 15

百度学术

15]}提出的Transformer网络模型,使得时序数据的预测性能得到了一定程度的提升,后相继提出了多种具有注意力机制的Transformer网络模型^{[参考文献 16

百度学术

16参考文献 ⇓-18

⇓-18]}。但由于Transformer模型的点稀疏形式的注意力机制以及其二次复杂度的问题,即增加了时间复杂度又限制了其对上下文时序信息的深度挖掘,且Transformer模型直接多步预测,虽然能捕捉较长期的趋势^{[参考文献 18

百度学术

18]},但却不利于捕捉序列的细节特点,尤其是在短时间变化快的时间序列上。综合上述分析,现有的时间序列模型普遍存在或多或少的问题,难以同时对现实中多种复杂的时序数据得到稳定优越的预测结果。因此,如何进一步提升数据在时序关联性上的提取能力,以满足对现代多种复杂时序数据预测的应用需求,仍是一个具有挑战性的任务。

译

针对上述问题,笔者提出了一种基于时间注意力机制双向长短期记忆网络的时间序列预测方法。基于改进的双向长短期记忆网络提取深度时间序列特征,挖掘深度时间序列特征的上下文时序依赖关系,并融合时间注意力机制,对深度时间序列特征进行自适应加权,提升深度时序特征的显著性表达能力。通过在多个时间序列数据集与同类代表性方法的多指标客观定量对比,验证了该方法的可行性和优越性。

译

2 时间注意力机制长短期记忆网络

基于已知时间序列数据预测未来时间的数据序列,构建基于时间注意力机制双向长短期记忆网络模型——TA-LSTM,其框架如图1所示。

译

图1 基于TA-LSTM的时间序列预测框架

下载: 原图 | 高精图 | 低精图

文中通过自回归生成方法,使用历史观测数据,迭代预测未来的状态空间。设原始时间序列长度为l+p,取前l项历史数据为模型输入I₁={X₁,X₂,…,X_l},后p个数据为预测结果的真实值O={X_l₊₁,X _l₊₂,…,X_l₊_p}。其中,X_l∈R^m,m为特征维度。经过一次TA-LSTM时间序列预测网络模型后,输出未来时刻的数据信息为X'_n₊₁,将输出结果添加至原始输入时间序列I的尾部,并相应去除X₁,以得到下一时刻的输入时序序列I₂={X₂,X₃,…,X' ${_{l +}}_{1}$ },反复迭代直到预测出后p项数据$\hat{\boldsymbol{O}}=\left\{\boldsymbol{X}_{l+1}^{\prime}, \boldsymbol{X}^{\prime}{ }_{H+2}, \cdots, \boldsymbol{X}_{l+p}^{\prime}\right\}$。通过上述迭代,TA-LSTM模型以滑动窗口的形式预测未来时间序列。

译

框架中TA-LSTM网络模型结构的详细预测过程,如图2所示。假设输入长度I₁={X₁,X₂,X₃,X₄},预测X'₅,其中X_i∈R^m,m为特征维度。首先将原始序列I₁,依据时间的先后顺序输入BLSTM,经过正向和反向信息的提取后,将信息输入LSTM进一步提取时间依赖关系。同时,为增强不同时序特征对当前预测序列的显著性表达,设计时间注意力机制,实现对深度时间序列特征进行自适应加权,得到预测结果X'₅。

译

图2 TA-LSTM网络结构示意图

下载: 原图 | 高精图 | 低精图

LSTM通过引入控制门(Gate)和记忆细胞(Memory Cell),获取时间序列数据的时序依赖,其网络结构如图3所示。

译

图3 LSTM网络结构示意图

下载: 原图 | 高精图 | 低精图

LSTM网络结构中,X_t和Y_t分别代表在t时刻模型的输入信息和输出信息,C_t和H_t则分别代表LSTM模型的细胞状态(Cell State)和隐藏状态(Hidden State)。Z_fZ_i和Z_o分别代表遗忘门(Forget Gate),输入门(Input Gate)和输出门(Output Gate),采用矩阵乘积和激活函数运算得到各个控制门的状态。Z_c则是将输入X_t经过tanh函数非线性激活后得到的临时细胞状态,代表历史输入信息的累积。b_f,b_i,b_o和b_c分别代表偏置项。其中,Z_f,Z_i,Z_o,Z_c以及C_t的计算公式如式(1)所示:

译

\{\begin{array}{l} Z_{f} = σ (W_{x f} \times X_{t} + W_{h f} \times H_{t - 1} + b_{f}), \\ Z_{i} = σ (W_{x i} \times X_{t} + W_{h i} \times H_{t - 1} + b_{i}), \\ Z_{o} = σ (W_{x o} \times X_{t} + W_{h o} \times H_{t - 1} + b_{o}), \\ Z_{c} = σ (W_{x c} \times X_{t} + W_{h c} \times H_{t - 1} + b_{c}), \\ C_{t} = Z_{f} \times C_{t - 1} + Z_{i} \times Z_{c}, \end{array}

(1)

其中,×为矩阵乘积,+为矩阵相加,σ(·)为sigmoid激活函数,tanh(·)为tanh激活函数。

译

LSTM模型通过当前输入X_t和之前输入对本次输入所产生的影响H_t_-1决定序列的输出Y_t,并通过训练学习细胞状态C_t决定输入X_t对下次输出影响程度H_t。其中,LSTM模型的输出Y_t可表示为

译

$\boldsymbol{Y}_{t}=\boldsymbol{H}_{t}=\boldsymbol{Z}_{o} * \tanh \left(\boldsymbol{C}_{t}\right)$,

(2)

其中,*为Hadamard积。

译

为获取更多的相关性信息,将输入序列同时输送到正向传播和反向传播的两个LSTM单元中,再将两个单元的输出结果拼接得到BLSTM的输出结果Y'_t,可表示为

译

, $\text{[math]}$

(3)

其中,和$\overleftarrow{\boldsymbol{Y}}_{t}$分别代表正向传播和反向传播在t时刻的输出结果。 inlinegraphic

译

将Y'_t作为中间变量输入TA-LSTM中LSTM单元,由式(2)得到LSTM输出的结果Y_f。

译

BLSTM模型虽然可兼顾前后时间信息,但由于时间序列各时刻的特征与当前预测值的关联程度不同,直接将正向和反向LSTM提取到的特征信息拼接作为预测结果,使BLSTM对所有信息的重视程度是相同的,易导致预测结果出现偏差。由于LSTM时序捕捉能力较强,选择在BLSTM提取的特征的同时,通过嵌入LSTM进一步提取时序上的信息,得到更深层次的时序依赖关系。同时,为增强不同时序特征对当前预测序列的显著性表达,基于上述可正向和反向传播的LSTM网络模型,设计基于时间注意力机制的网络模型TA-LSTM,实现对深度时间序列特征进行自适应加权。

译

针对自适应加权的注意力机制,相关学者在文本分类^[

19]和学术场所推荐^{[参考文献 20

百度学术

20]}上进行了应用研究。这种采用全连接层学习输入信息对当前信息所作的相对贡献取得了较好的效果。延续其自适应加权的思路,并对注意力机制改进,使其适用于时间序列预测。

译

考虑时间序列在时序上的关联性,将经过BLSTM和LSTM网络后的输出特征Y_f视作注意力层的输入特征,采用tanh函数激活,使输入序列信息更加平稳,以保证更合理的分配权重。接着,经过归一化后的输入与注意力参数矩阵ω^T相乘,加上偏置权重b经Softmax函数非线性激活,得到窗口内时间序列特征的权重得分S_t。通过矩阵广播机制,将得分S_t与原输入特征进行Hadamard乘积,得到注意力输出结果H'_a。其中,S_t和H'_a的计算公式如式(4)和式(5)所示

译

$\boldsymbol{S}_{t}=\operatorname{Softmax}\left(\boldsymbol{\omega}^{\mathrm{T}} \times \tanh \left(\boldsymbol{Y}_{f}\right)+\boldsymbol{b}\right)$,

(4)

$\boldsymbol{H}_{a}^{\prime}=\boldsymbol{Y}_{f} * \boldsymbol{S}_{t}$,

(5)

其中,Y_f∈Rⁿ^×^d 为TA-LSTM中LSTM层的输出结果,n为输入序列长度,d为隐藏层的输出个数。

译

参数矩阵ω^T在网络模型训练时,通过反向传播算法更新其参数,Softmax函数计算为

译

Softmax(X_i)=

\frac{e^{x_{i}}}{\overset{n}{\sum_{j = 1}} e^{x_{j}}}

。

(6)

H'_a相加求和并经过全连接层得到注意力机制的最终输出结果。

译

时间注意力在LSTM层提取时序信息后,通过式(4),计算得到可以适应不同时刻的权重得分S_t。随后,不同的权重得分S_t对LSTM提取到的时序信息进行加权,自适应地增强不同时序特征对当前预测序列的显著性表达。

译

3 实验结果与分析

为测试TA-LSTM网络模型对时间序列数据的预测性能,选择LightGBM^[

9]、LSTM^{[参考文献 11

百度学术

11]}、BLSTM^{[参考文献 13

百度学术

13]}、BLSTM-L^{[参考文献 14

百度学术

14]}以及Transformer^{[参考文献 17

百度学术

17]}等同类代表性网络模型,分别在羽毛球竞技动作时序数据集和两个公开数据集AirQuality^{[参考文献 21

百度学术

21]}、Power^{[参考文献 22

百度学术

22]}进行客观定量对比。同时,为了进一步验证文中所提出的注意力方法在时间序列预测上更加有效,笔者引入了基于文献[19]的时间注意力机制的BLSTM的方法(Att-BLSTM)作为模型的对比实验。实验平台的硬件配置为:Intel i7-6700 CPU,Nvidia Geforce 1070ti GPU。

译

3.1 数据集

羽毛球竞技动作时序数据集由羽毛球领域专业人士通过20位国际顶尖羽毛球运动员在多类国际赛事上的78场完整的羽毛球比赛数据记录而成,包含6 311回合的技术动作时间序列;AirQuality^[

21]为意大利空气质量数据集;Power^{[参考文献 22

百度学术

22]}为法国巴黎家庭用电量数据集。

译

由于时间序列预测是在一个序列上的连续预测过程,基于历史数据的一次次迭代捕捉序列间隐藏的时间或顺序上的依赖关系,并依据这种依赖关系对未来未知序列进行预测。因此,文中采用滑动窗口^[

17-18]切片策略产生时间序列预测的输入数据。采用滑动窗口产生的数据,有利于TA-LSTM反复挖掘上下文的时序上的联系,进而捕捉这种依赖关系,实现对未来的预测。上述3个数据集为不同领域的时间序列数据,数据集特点如表1。在实验过程中,以7∶1∶2的比例划分训练集、验证集和测试集。

译

表1 不同数据集特点

数据集名称	类型	特征数	数据集长度
Badminton	国际羽毛球比赛数据	4	3 155 537
AirQuality^{[参考文献 21 百度学术 21]}	意大利空气质量数据	12	9 538
Power^{[参考文献 22 百度学术 22]}	法国家庭用电量数据	8	2 075 260

下载: CSV

其中,羽毛球竞技动作时序数据集(Badminton)的每一个序列由一个击打动作文本构成,包含击球位置(pos)、正反手(hand)、击球动作(tec)及击球路径(path)等4个维度特征,如表2。根据各个特征的离散取值数量建立词嵌入字典,对序列中的文本进行编码,从而转换成数值向量便于运算。

译

表2 Badminton数据集特征

特征	值	取值数量
pos	中中场,中前场,中后场…	9
hand	反手,头顶,正手	3
tec	劈吊,勾,吊,抽,接杀挑…	19
path	中路,斜线,直线	3

下载: CSV

由于上述4个特征取值较多,导致对应的编码数值波动较大,易造成梯度下降速度变缓,不利于深度学习模型收敛。针对上述问题,对上述特征分别进行归一化操作,将其数据分布缩放到[-1,1]区间内,其算式为

译

X_i=

\frac{X_{i} - (X_{m a x} + X_{m i n}) / 2}{(X_{m a x} - X_{m i n}) / 2}

(7)

其中,X_max为该特征数据的最大值,X_min为该特征数据的最小值。

译

3.2 参数选择和定量分析

为获取合理的TA-LSTM网络模型参数,在TA-LSTM网络模型的训练过程中,采用自监督学习方法。设时间序列总长度为L,以滑动窗口的方式,将训练数据划分(L-l-p)个序列作为训练数据进行使用。以击打动作序列长度即时间窗口长度为5为例,其由原始数据产生经过处理得到击打动作时间序列的过程如图4所示。将每回合羽毛球比赛序列滑动切片为若干个击打动作时间序列,将最后一个击打动作数值视为当前序列的预测标签T。

译

图4 滑动切片为击打动作时间序列示意图

下载: 原图 | 高精图 | 低精图

设TA-LSTM网络模型的输出值$\boldsymbol{y}=\left[\boldsymbol{y}_{1}, \boldsymbol{y}_{2}, \boldsymbol{y}_{3}, \boldsymbol{y}_{4}\right]$分别代表击球位置(pos)、正反手(hand)、击球动作(tec)及击球路径(path)等特征的预测值,采用如式(8)中所示的均方误差(Mean Squared Error,MSE)作为训练损失函数。

译

为获取最优TA-LSTM隐藏层神经元数,以64为步长,基于Badminton数据集,采用L_MSE做损失函数在[64,384]区间上讨论隐藏层神经元数目对TA-LSTM网络模型的预测性能,部分实验结果如图5所示。

译

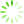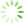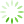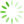
图5 基于Badminton数据集不同隐藏层神经元数的均方误差

下载: 原图 | 高精图 | 低精图

由图5可知,随着隐藏层神经元数目的增加,均方误差呈现下降趋势,当隐藏层神经元数为256时,均方误差最小,表明TA-LSTM网络模型已具有最优的预测性能;随着隐藏层神经元数目的增加,均方误差开始小幅度增长。因此,将TA-LSTM网络模型的隐藏层神经元数设置为256,并在后续的实验中保持不变。

译

由于羽毛球运动员的击打动作具有强的时序性,且与其已有的击打动作具有强的关联性。为获取最佳的击打动作序列长度,以1为步长,采用均方误差,分别在区间[3,6]上讨论击打动作序列长度对TA-LSTM网络模型的预测性能,部分实验结果如图6所示。

译

图6 基于Badminton数据集中不同动作序列长度的均方误差

下载: 原图 | 高精图 | 低精图

由图6可知,随着击打动作序列长度的增加,均方误差呈现下降趋势,当击打动作序列长度为5时,均方误差最小,表明TA-LSTM网络模型已具有最优的预测性能;随着击打动作序列长度的增加,均方误差开始小幅度增长。因此,将TA-LSTM网络模型的击打动作序列长度设置为5,并在后续的实验中保持不变。

译

为客观定量评价TA-LSTM网络模型的预测性能,基于上述Badminton数据集,分别采用均方误差、平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)和皮尔逊相关系数(Pearson Correlation Coefficient,PCC)进行综合评估,上述评价指标的计算为

译

\{\begin{array}{l} M S E = \frac{1}{m n} \overset{n}{\sum_{j = 1}} \overset{m}{\sum_{i = 1}} (y_{i}^{j} - {\hat{y}}_{i}^{j})^{2}, \\ M A E = \frac{1}{m n} \overset{n}{\sum_{j = 1}} \overset{m}{\sum_{i = 1}} | y_{i}^{j} - {\hat{y}}_{i}^{j} |, \\ R M S E = \frac{1}{n} \overset{n}{\sum_{j = 1}} {(\frac{1}{m} \overset{m}{\sum_{i = 1}} (y_{i}^{j} - {\hat{y}}_{i}^{j})^{2})}^{1 / 2}, \\ P C C = \frac{\overset{n}{\sum_{j = 1}} \overset{m}{\sum_{i = 1}} (y_{i}^{j} - {\bar{y}}_{i}^{j}) (y_{i}^{j} - {\overset{︿}{\bar{y}}}_{i}^{j})}{{(\overset{n}{\sum_{j = 1}} \overset{m}{\sum_{i = 1}} (y_{i}^{j} - {\bar{y}}_{i}^{j}))}^{1 / 2} {(\overset{n}{\sum_{j = 1}} \overset{m}{\sum_{i = 1}} (y_{i}^{j} - {\overset{︿}{\bar{y}}}_{i}^{j}))}^{1 / 2}}, \end{array}

(8)

其中,m代表特征维度,n为训练样本个数, $y_{i}^{j}$ 代表第j个训练样本的第i个特征的实际值, ${\hat{y}}_{i}^{j}$ 代表第j训练个样本的第i个特征的预测值。

译

部分实验结果如表3所示。其中,最优预测性能结果以粗体显示,箭头指向代表评价指标较优性能趋势。表3结果可以看出,TA-LSTM网络模型在Badminton数据集上,各项评价指标均优于LSTM^[

12],BLSTM^{[参考文献 13

百度学术

13]}、BLSTM-L^{[参考文献 14

百度学术

14]}等同类代表性网络模型,尤其是在MAE和RMSE分别提升1.3%和3.1%,表明文章所提出的TA-LSTM网络模型方法具有优异的预测性能。

译

表3 不同网络模型在Badminton数据集预测结果

网络模型	评价指标
网络模型	MAE↓	MSE↓	RMSE↓	PCC↑
LightGBM^{[参考文献 9 百度学术 9]}	0.438	0.558	0.491	0.704
LSTM^{[参考文献 12 百度学术 12]}	0.243	0.372	0.342	0.883
BLSTM^{[参考文献 13 百度学术 13]}	0.227	0.327	0.296	0.896
BLSTM-L^{[参考文献 14 百度学术 14]}	0.226	0.324	0.290	0.905
Transformer^{[参考文献 17 百度学术 17]}	0.232	0.387	0.305	0.887
Att-BLSTM^{[参考文献 19 百度学术 19]}	0.228	0.326	0.297	0.899
TA-LSTM(文中方法)	0.223	0.323	0.281	0.904

下载: CSV

在测试集上,取4组击打时间序列长度为5的数据为一个批量(batch size),得到输入序列、注意力机制的输入特征热力图、注意力机制得分S_t以及模型标签及预测结果对比,如图7所示。

译

图7 部分结果展示

下载: 原图 | 高精图 | 低精图

由图7可以看出:输入模型的特征经过BLSTM和LSTM之后特征数量增加,进而可以获得更高层次的特征信息。其中,热力图代表各特征的取值,取值越高,代表其对预测结果的影响就越大。矩阵S_t的每一行代表其在不同时刻输入时的权重,高层次的特征信息经注意力机制的得分S_t对每个输入序列的每个时间步长进行加权,进一步加深前后时序对当前时序在时间上的依赖关系。同时,TA-LSTM在不同输入时,注意力机制的权重得分S_t是实现了自适应加权,进而得到更优的预测结果。

译

为进一步验证TA-LSTM网络模型的预测性能,分别在AirQuality^[

21]和Power^{[参考文献 22

百度学术

22]}不同领域的长时间序列数据集上进行定量对比实验,部分实验结果如表4所示。

译

表4 不同网络模型在AirQuality^{[参考文献 21

百度学术

21]}与Power^{[参考文献 22

百度学术

22]}数据集的预测结果

网络模型	AirQuality^{[参考文献 21 百度学术 21]}				Power^{[参考文献 21 百度学术 21]}
网络模型	MAE↓	MSE↓	RMSE↓	PCC↑	MAE↓	MSE↓	RMSE↓	PCC↑
LightGBM^{[参考文献 9 百度学术 9]}	0.649	0.727	0.693	0.803	0.450	0.534	0.478	0.716
LSTM^{[参考文献 12 百度学术 12]}	0.423	0.670	0.646	0.910	0.163	0.391	0.319	0.823
BLSTM^{[参考文献 13 百度学术 13]}	0.426	0.678	0.651	0.902	0.179	0.424	0.345	0.826
BLSTM-L^{[参考文献 14 百度学术 14]}	0.432	0.674	0.664	0.878	0.177	0.407	0.332	0.816
Transformer^{[参考文献 17 百度学术 17]}	0.461	0.809	0.708	0.901	0.184	0.390	0.350	0.824
Att-BLSTM^{[参考文献 19 百度学术 19]}	0.488	0.867	0.766	0.837	0.174	0.381	0.320	0.827
TA-LSTM(文中方法)	0.397	0.596	0.626	0.922	0.166	0.370	0.318	0.832

下载: CSV

由表4可以看出,文中所提出的TA-LSTM网络模型在AirQuality^[

21]和Power^{[参考文献 22

百度学术

22]}数据集上的预测性能,除在Power^{[参考文献 22

百度学术

22]}数据集上的MAE指标略低于LSTM外,其他各项性能指标均优于LSTM^{[参考文献 11

百度学术

11]},BLSTM^{[参考文献 13

百度学术

13]}、BLSTM-L^{[参考文献 14

百度学术

14]}、Transformer^{[参考文献 17

百度学术

17]}和Att-BLSTM^{[参考文献 19

百度学术

19]}等网络模型,尤其是在AirQuality^{[参考文献 21

百度学术

21]}上MAE、MSE、RMSE和PCC分别提升6.1%、11%、3%和1.2%。结果表明文中提出的TA-LSTM网络模型具有优异的时间序列预测性能和较强的泛化能力,可适用于多种不同类别的复杂时间序列数据预测。

译

在现有的时间序列预测方法上,机器学习方法大多适用于单变量预测,在处理多变量协同的多元时间预测上难以发现时序上的关系;基于Transformer的方法更适用于捕捉多元变量的长期趋势关系,但点稀疏形式的注意力限制了其对上下文时序信息的深度挖掘;而基于LSTM的对比方法存在或多或少的对时序重视程度以及深层次特征提取的问题。因此,这些现有的模型都难以同时满足对现实中多种复杂的时序数据预测的应用需求。TA-LSTM网络模型采用正向和反向传播机制提取时序信息,并经过LSTM进一步得到深度时序特征依赖关系,最终通过自适应权重分配策略,使得TA-LSTM网络模型对于不同时序信息的拟合度高,从而避免了因时间序列上下文不一致导致的依赖信息丢失问题。因此,模型在实验上表现出较优的预测性能和较强的泛化能力。

译

3.3 消融实验

为了验证TA-LSTM各组件对模型整体贡献,文中继续对模型进行消融实验。分别对文中贡献最大的3个组件:时间注意力机制(Time Attention)、提取深度时序特征依赖关系的LSTM模块以及主干网络BLSTM进行3组不同的消融实验。本次实验在Badminton数据集上进行预测,(w/o)表示去除某个模块后TA-LSTM剩余部分的模型,其实验结果如表5所示。

译

表5 在Badminton上的消融实验结果

方法	Badminton
方法	MSE↓	MAE↓	RMSE↓	PCC↑
(w/o) Time Attention	0.236	0.365	0.301	0.890
(w/o) BLSTM	0.228	0.325	0.293	0.901
(w/o) LSTM	0.225	0.325	0.297	0.904
TA-LSTM	0.223	0.323	0.281	0.904

下载: CSV

由表5可以得出以下结论:(1)去除时间注意力机制的影响最大。这表明时间注意力机制的自适应加权融合可以为模型提供更好的特征提取能力,可以帮助模型精准预测出未来的变化趋势。(2)去除BSLTM时模型的性能大幅降低。这表明采用正向和反向传播机制能有效地捕捉时间序列中潜在的时序依赖信息。(3)LSTM负责在BLSTM后得到更深层次的时序特征依赖关系,去除LSTM后模型得不到较强的时序依赖关系,进而出现预测结果的偏差。TA-LSTM各组件的相互组合,使得模型预测的结果更加准确。其通过BLSTM提取到双向的时序特征,由LSTM进行深度时序特征的提取,最终通过时间注意力机制的自适应加权融合,得到更加接近真实值的预测序列。消融实验再次验证了文中所提出模型在理论和实践上的合理性和优越性。

译

4 结束语

笔者提出了一种基于时间注意力机制双向长短期记忆网络的时间序列预测方法,基于双向长短期记忆网络提取深度时间序列特征,挖掘上下文的时序依赖关系。采用融合时间注意力机制策略,对深度时间序列特征进行自适应加权,提升深度时序特征的显著性表达能力。通过与同类代表性网络模型在多个不同时间序列数据集上的客观定量对比,结果表明该方法可以预测多种复杂的现代时间序列数据任务,具有较强的泛化性和优异的时序预测性能。为提高TA-LSTM的性能,未来将面向更多领域的复杂时间序列数据,对模型做进一步的完善和优化

译

参考文献

[1]

KOWSARI K, MEIMANDI K J, HEIDARYSAFA M, et al. Text Classification Algorithms:A Survey[J]. Information, 2019, 10(4):150-172. [百度学术]

[2]

DURAIRAJ D M, MOHAN B H K. A Convolutional Neural Network Based Approach to Financial Time Series Prediction[J]. Neural Computing and Applications, 2022, 34(16):13319-13337. [百度学术]

[3]

CAMASTRA F, CAPONE V, CIARAMELLA A, et al. Predictionof Environmental Missing Data Time Series by Support Vector Machine Regression and Correlation Dimension Estimation[J]. Environmental Modelling & Software, 2022, 150:1043-1053. [百度学术]

[4]

刘惠, 董锡耀, 杨志涵. 融合Stacking框架的BiGRU-LGB云负载预测模型[J]. 西安电子科技大学学报, 2023, 50(3):83-94. [百度学术]

LIU Hui, DONG Xiyao, YANG Zhihan. Bigru-LGB Cloud Load Prediction Model Incorporating Stacking Framework[J]. Journal of Xidian University, 2023, 50(3):83-94. [百度学术]

[5]

张梦迪, 徐庆, 刘振鸿, 等. 基于动态滑动窗口BP神经网络的水质时间序列预测[J]. 环境工程技术学报, 2022, 12(3):809-815. [百度学术]

ZHANG Mengdi, XU Qing, LIU Zhenhong, et al. Water Quality Time Series Prediction Based on Dynamic Sliding Window BP Neural Network[J]. Journal of Environmental Engineering Technology, 2022, 12(3):809-815. [百度学术]

[6]

MOHANTY M K, THAKURTA P K G, KAR S. Agricultural Commodity Price Prediction Model:A Machine Learning Framework[J]. Neural Computing and Applications, 2023, 35(20):15109-15128. [百度学术]

[7]

YULE G U. On A Method of Investigating Periodicities Disturbed Series,with Special Reference to Wolfer's Sunspot Numbers[J]. Philosophical Transactions of the Royal Society of London.Series A,Containing Papers of a Mathematical or Physical Character, 1927, 226(636-646):267-298. [百度学术]

[8]

WALKER G T. On Periodicity in Series of Related Terms[J]. Proceedings of the Royal Society of London.Series A,Containing Papers of a Mathematical and Physical Character, 1931, 131(818):518-532. [百度学术]

[9]

CHO C, KWON K, WU C. On Weather Data-Based Prediction of Gamma Exposure Rates Using Gradient Boosting Learning for Environmental Radiation Monitoring[J]. Sensors, 2022, 22(18):7062. [百度学术]

[10]

LIU S, FU B, WANG W, et al. Dynamic Sepsis Prediction for Intensive Care Unit Patients Using Xgboost-Based Model with Novel Time-Dependent Features[J]. IEEE Journal of Biomedical and Health Informatics, 2022, 26(8):4258-4269. [百度学术]

[11]

SIŁKA J, WIECZOREK M, WOŁNIAK M. Recurrent Neural Network Model for High-Speed Train Vibration Prediction from Time Series[J]. Neural Computing and Applications,2022,34(16):13305-13318. [百度学术]

[12]

HOCHREITER S, SCHMIDHUBER J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8):1735-1780. DOI:10.1162/neco.1997.9.8.1735 [百度学术]

[13]

HAFEZI L, REZAEIAN M. Neural Architecture for Persian Named Entity Recognition[C]//Proceedings of 4th Iranian Conference on Signal Processing and Intelligent Systems. Piscataway:IEEE, 2018:61-64. [百度学术]

[14]

KAUSHIK P, GUPTA A, ROY P P, et al. EEG-Based Age and Gender Prediction Using Deep BLSTM-LSTM Network Model[J]. IEEE Sensors Journal, 2019, 19(7):2634-2641. DOI:10.1109/JSEN.2018.2885582 [百度学术]

[15]

VASWANI A, SHAZEER N, PARMAR N, et al. Attention Is All You Need[J]. Advances in Neural Information Processing Systems, 2017, 30:2171-2184. [百度学术]

[16]

KITAEV N, KAISER Ł, LEVSKAYA A. Reformer:The Efficient Transformer[C]//Proceedings of 9th International Conference on Learning Representations. La Jolla: ICLR, 2020:1-12. [百度学术]

[17]

ZERVEAS G, JAYARAMAN S, PATEL D, et al. A Transformer-Based Framework for Multivariate Time Series Representation Learning[C]//Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. New York: ACM, 2021:2114-2124. [百度学术]

[18]

ZHOU H, ZHANG S, PENG J, et al. Informer:Beyond Efficient Transformer for Long Sequence Time-Series Forecasting[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2021:11106-11115. [百度学术]

[19]

LIU G, GUO J. Bidirectional LSTM with Attention Mechanism and Convolutional Layer for Text Classification[J]. Neurocomputing, 2019, 337:325-338. [百度学术]

[20]

PRADHAN T, KUMAR P, PAL S. CLAVER:An Integrated Framework of Convolutional Layer,Bidirectional LSTM with Attention Mechanism based Scholarly Venue Recommendation[J]. Information Sciences, 2021, 559:212-235. [百度学术]

[21]

AGARWAL N, BRUKHIM N, HAZAN E, et al. Boosting for Control of Dynamical Systems[C]//Proceedings of International Conference on Machine Learning. New York: PMLR, 2020:96-103. [百度学术]

[22]

GASPARIN A, LUKOVIC S, ALIPPI C. Deep Learning for Time Series Forecasting:The Electric Load Case[J]. CAAI Transactions on Intelligence Technology, 2022, 7(1):1-25. [百度学术]

摘要

时间序列预测即利用历史时间序列数据

预测未来一段时间内的数据信息

以便提前制定相应策略。目前

时间序列的类别复杂繁多

而现有的时间序列预测模型面对多种类型数据时无法取得稳定预测的结果

进而难以同时满足对现实中多种复杂的时序数据预测的应用需求。针对上述问题

提出了一种基于时间注意力机制双向长短期记忆网络的时间序列预测方法。笔者提出的网络模型采用改进的正向和反向传播机制提取时序信息并通过自适应权重分配策略推理未来的时序信息。具体来说

设计了一个改进的双向长短期记忆网络

通过结合双向长短期记忆和长短期记忆网络提取深度时间序列特征

挖掘上下文的时序依赖关系。在此基础上

融合所提出的时间注意力机制

实现对深度时间序列特征进行自适应加权

提升深度时序特征的显著性表达能力。通过与同类代表性方法在多个不同类别数据集上的客观定量对比

实验结果表明

该方法能够在多种类别的复杂时间序列数据上更优的预测性能。

Abstract

Time series prediction means the use of historical time series to predict a period of time in the future

so as to formulate corresponding strategies in advance.At present

the categories of time series are complex and diverse.However

existing time series prediction models cannot achieve stable prediction results when faced with multiple types of time series data.The application requirements of complex time series data prediction in reality are difficult to simultaneously meet.To address the problem

a time series prediction method is proposed based on the Bidirectional Long and Short-term Memory(BLSTM) with the attention mechanism.The improved forward and backward propagation mechanisms are used to extract temporal information.The future temporal information is inferred through an adaptive weight allocation strategy.Specifically

an improved BLSTM is proposed to extract deep time series features and explore temporal dependencies of context by combining BLSTM and Long Short-term Memory(LSTM) networks

on the basis of which the proposed temporal attention mechanism is fused to achieve adaptive weighting of deep time series features

which improves the saliency expression ability of deep time series features.Experimental results demonstrate that the proposed method has a superior prediction performance in comparison with some representative methods in multiple time series datasets of different categories.

关键词

时间序列双向长短期记忆网络长短期记忆网络注意力机制深度学习

Keywords

time seriesBidirectional Long Short-Term MemoryLong Short-Term Memoryattention mechanismdeep learning

references

KOWSARI K, MEIMANDI K J, HEIDARYSAFA M, et al. Text Classification Algorithms:A Survey[J]. Information, 2019, 10(4):150-172.

DURAIRAJ D M, MOHAN B H K. A Convolutional Neural Network Based Approach to Financial Time Series Prediction[J]. Neural Computing and Applications, 2022, 34(16):13319-13337.

刘惠, 董锡耀, 杨志涵. 融合Stacking框架的BiGRU-LGB云负载预测模型[J]. 西安电子科技大学学报, 2023, 50(3):83-94.

LIU Hui, DONG Xiyao, YANG Zhihan. Bigru-LGB Cloud Load Prediction Model Incorporating Stacking Framework[J]. Journal of Xidian University, 2023, 50(3):83-94.

张梦迪, 徐庆, 刘振鸿, 等. 基于动态滑动窗口BP神经网络的水质时间序列预测[J]. 环境工程技术学报, 2022, 12(3):809-815.

MOHANTY M K, THAKURTA P K G, KAR S. Agricultural Commodity Price Prediction Model:A Machine Learning Framework[J]. Neural Computing and Applications, 2023, 35(20):15109-15128.

WALKER G T. On Periodicity in Series of Related Terms[J]. Proceedings of the Royal Society of London.Series A,Containing Papers of a Mathematical and Physical Character, 1931, 131(818):518-532.

CHO C, KWON K, WU C. On Weather Data-Based Prediction of Gamma Exposure Rates Using Gradient Boosting Learning for Environmental Radiation Monitoring[J]. Sensors, 2022, 22(18):7062.

SIŁKA J, WIECZOREK M, WOŁNIAK M. Recurrent Neural Network Model for High-Speed Train Vibration Prediction from Time Series[J]. Neural Computing and Applications,2022,34(16):13305-13318.

HOCHREITER S, SCHMIDHUBER J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8):1735-1780. DOI:10.1162/neco.1997.9.8.1735http://doi.org/10.1162/neco.1997.9.8.1735

HAFEZI L, REZAEIAN M. Neural Architecture for Persian Named Entity Recognition[C]//Proceedings of 4th Iranian Conference on Signal Processing and Intelligent Systems. Piscataway:IEEE, 2018:61-64.

VASWANI A, SHAZEER N, PARMAR N, et al. Attention Is All You Need[J]. Advances in Neural Information Processing Systems, 2017, 30:2171-2184.

KITAEV N, KAISER Ł, LEVSKAYA A. Reformer:The Efficient Transformer[C]//Proceedings of 9th International Conference on Learning Representations. La Jolla: ICLR, 2020:1-12.

LIU G, GUO J. Bidirectional LSTM with Attention Mechanism and Convolutional Layer for Text Classification[J]. Neurocomputing, 2019, 337:325-338.

AGARWAL N, BRUKHIM N, HAZAN E, et al. Boosting for Control of Dynamical Systems[C]//Proceedings of International Conference on Machine Learning. New York: PMLR, 2020:96-103.

GASPARIN A, LUKOVIC S, ALIPPI C. Deep Learning for Time Series Forecasting:The Electric Load Case[J]. CAAI Transactions on Intelligence Technology, 2022, 7(1):1-25.

117

浏览量

下载量

CSCD

文章被引用时，请邮件提醒。

提交

工具集

关联资源

三维注意力增强的暴力场景检测算法

融合超分辨率重建技术的多尺度目标检测算法

融合上下文感知注意力的低光图像去雾网络

注意力机制的SAR图像车辆目标检测网络

一种用于自动驾驶场景的轻量级语义分割网络